Его объем будет

?
Правильно (только заключать формулы в доллары не забывайте).
Соответственно, если все такие объемы сложить, получится интересующий нас объем тела вращения. Пишем:

А теперь вспоминаем историю. Когда-то кое-кто догадался, что если в подобной сумме слагаемые будут очень маленькими (если диски - очень тонкие), то ее можно будет вычислить, не складывая все многочисленные слагаемые непосредственно, а воспользовавшись другими, более удобными методами. При этом, правда, принято вместо

писать

, а вместо греческой буквы

записывать латинскую

, правда, сильно вытянутую по вертикали, вот так:
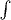
. Если мы сделаем соответствующие переобозначения, то у нас получится следующее:

Осталось немного. Вместо записи "по всем дискам" в подобной ситуации принято писать, от какого и до какого значения меняется координата очередного диска

. Вот так:

Все. Интеграл берите сами, насколько я понимаю, это Вы делать умеете. А на будущее запомните (надеюсь, математики меня не сильно за это побьют): в подобных задачах, равно как и во многих других приложениях интегрального исчисления, интеграл - это
сумма большого числа маленьких слагаемых, в которой принято писать ту самую закорюку вместо буквы

. Если Вы это хорошо осознаете, то никакие готовые "формулы для вычисления объемов" Вам уже не понадобятся, их можно будет выписывать самостоятельно для каждой конкретной задачи и в том виде, в котором они для данной задачи удобнее.



