Существует функция

, которая показывает, как растет число простых чисел на числовом ряду.
Данная работа исследует путь (не формулу, а алгоритм), которому в известной мере подчиняется

.
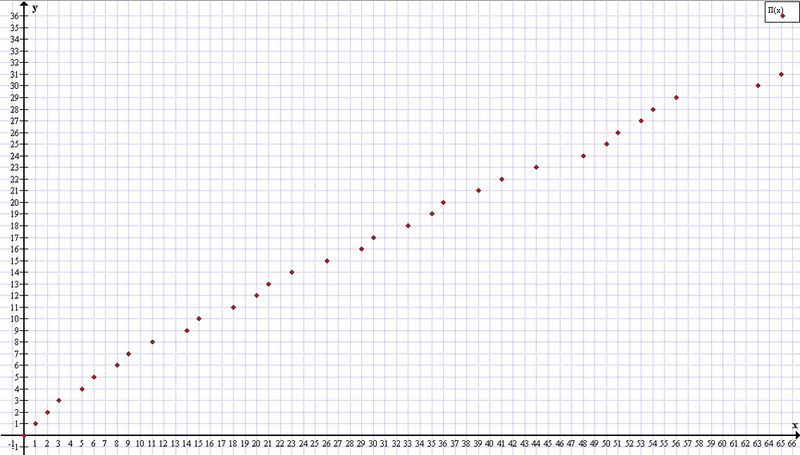
Рис. 1.
Здесь и далее на графиках по оси

показаны только нечетные числа. В точке

располагается

.
Если обозначить координату по оси

как

, то

.
где

- нечетное целое.
При больших числах функция ведет себя достаточно предсказуемо. В общих чертах является обратной логарифму числа. Есть достаточно точная функция Римана и другие.
В данной работе я попытаюсь определить некоторые закономерности, которые свойственны этой функции в начале числового ряда, а также покажу, в какой степени эти закономерности применимы для нечетных чисел (до

).
Чтобы описать поведение функции в математике достаточно знать ее производную. Затем, суммируя производные, можно получить и значение самой функции.
Также, если бы мы знали производную для функции

мы могли бы получить и саму функцию.
Попробуем определить производную для

.
Назовем эту функцию

, а ее сумму

.
Сравнение между собой

и

позволит сказать, насколько точно мы определили исходные параметры распределения простых чисел.
Я не буду расписывать все в мельчайших подробностях, а буду так сказать «рисовать широкой кистью».

– характеризует наклон функции

для числа

и соответствует комбинаторной вероятности того, что исследуемое число не содержит в себе меньших простых множителей (является простым).
Мы вправе ожидать, что всякий раз после появления числа - такого, например, как

- последующие числа будут иметь возможность делиться на

. И так действительно происходит (

или

).
Примечание. Такие числа, как

хоть и делятся на

, но не «выключают неизвестные». Т.е. можно сказать, что до своего квадрата простое число зависит от меньших простых.
Элементарная логика подсказывает, что если до

числа уже могли делиться на

, тогда множители

и

займут свои места на числовом ряду и ограничат число неделящихся на эти множители числа следующим соотношением:

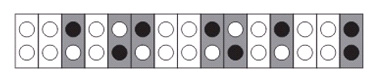
Рис. 2.
В реальности это не совсем так. Дело в том, что

входит в цикл по

НЕСИММЕТРИЧНО! Не в начале цикла по

. А именно вот так:
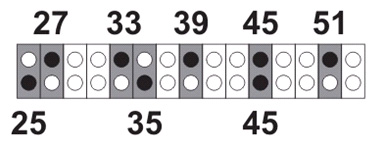
Рис. 3.
Можно заметить, что в начале нового цикла от


окажется меньше (светлых прямоугольников меньше, чем в целом на цикле). Так происходит всегда и это легко показать.
Наиболее логичным выглядит предположение, что полноценный (симметричный) цикл для нескольких делителей начинается с момента их совпадения – кратного числа (в данном случае для чисел

и

полноценный цикл начнется только после числа

). А до этого мы должны использовать для чисел от

до

включительно:

Итак, после встречи с квадратом простого числа у нас есть 2 варианта:
1 вариант (элементарная логика).

, и тогда

2 вариант (пересчет до начала "симметричного" цикла).

, и тогда

После «45» никаких перекосов уже не будет. Цикл выровняется, станет «симметричным».
Видна существенная разница. Правильным является искать кратные, вычислять вероятность (комбинаторную) простых чисел до кратного, суммировать ее, но это связано с существенными вычислительными трудностями.
Существует и 3 вариант. «ОБНУЛИТЬ ЦИКЛ»3 основных правила.
1). После появления квадрата простого числа нужно начинать новый цикл. Чтобы это сделать, нужно как бы начать все заново. Чтобы обнулить данные, нужно присвоить квадрату вероятность

.
Тогда будем иметь:
Предшествующий цикл заканчивается в своем «псевдо-случайном месте».
Следующий цикл начинается с «псевдо-случайного места».
При больших числах квадратов вероятности должны друг друга компенсировать.
Имеем число (квадрат), у которого вероятность быть простым равна

.
2). Если мы присвоим какому-либо квадрату вероятность

, то на какое число мы бы его ни умножили и какое бы число после этого не получили, для этого нового числа также будет

.
3). Квадрат числа

входит на числовой ряд симметрично. Он не зависит ни от каких других чисел (кроме

быть может, от которого также зависят все другие числа). Это придает ему особые свойства.
Примечание. Так называемые «близнецы» - это «реликтовое излучение» от самых первых циклов по

.
Припишем первые вероятности  .
. 
, поскольку

является собственным квадратом,
а значит график начинается из точки

;


;

и т.д.
Припишем  числам второго уровня (я бы назвал их составными или «грязными» квадратами).
числам второго уровня (я бы назвал их составными или «грязными» квадратами). 
,

,

,

, …

;

,

,

,

, …

;
и т.д.
Вероятности чисел c  не равной
не равной  будем считать по обычной комбинаторной формуле, например:
будем считать по обычной комбинаторной формуле, например: 

Пока отложим нахождение составных (грязных) квадратов по

, (связанных с Правилом 3., далее Фактор-9), и посмотрим, что у нас получится, если посчитать

для каждого числа (без учета Фактора-9) и просуммировать их.
Я составил программу для вычислений

с учетом вышеприведенных правил, и их суммирования в

на языке Pascal для нечетных чисел не больше

(а точнее до последнего простого, равного

перед

).
Нужно отметить, что для вычислений до

нам понадобится знать все простые до корня из

, а именно до

включительно.
Данные помещаю в программу GRAPH (графики) и Excel (таблицы).
Итак, что я делаю. Беру число, например,

, проверяю его, является ли оно "квадратом" или "грязным квадратом" и если не является, присваиваю

Беру другое число, например,

проверяю его - он0 оказывается "грязным квадратом" - присваиваю

.
Затем суммирую на интервале от

и до


и получаю

. В принципе, интервал не обязательно начинать с

. Алгоритм работает независимо от начала.
Смотрю, насколько

похожа на

.
График 1. Рис. 1. (масштабированный, для удобства визуализации)
без учета Фактора-9 – зеленая линия,
и

распределения простых чисел – красная линия.
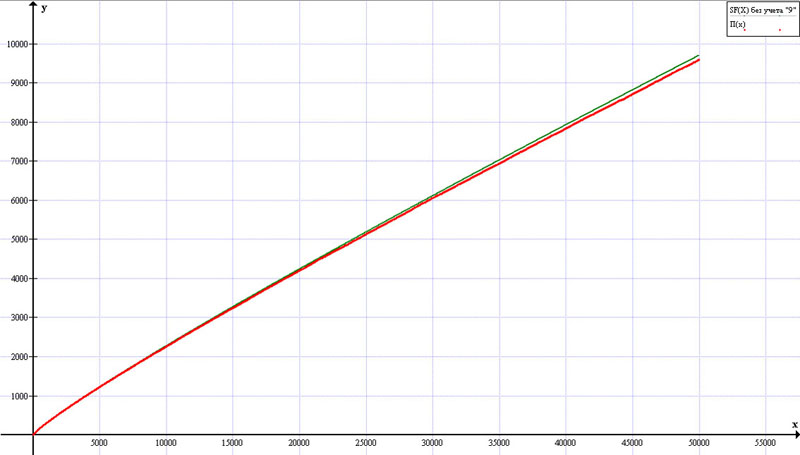 График 1. Рис. 2. (немасштабированный, начало ряда)
График 1. Рис. 2. (немасштабированный, начало ряда)
без учета Фактора-9 – зеленая линия,
и

распределения простых чисел – красная линия.
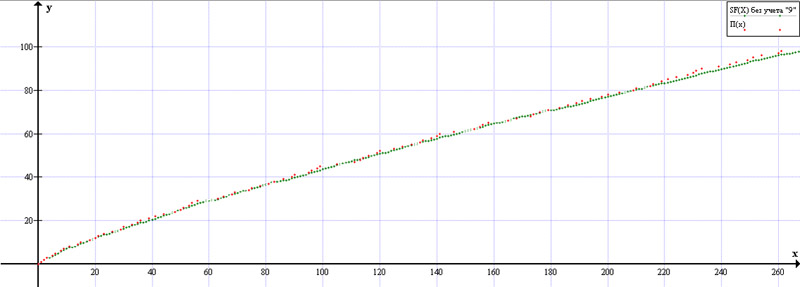
Видно, что

достаточно точно отображает поведение функции

на начальном этапе, а ближе к концу отклоняется. Получается прогноз

больше, чем

.
Это связано с неучтением Фактора-9 и его производных.
Если по большим, «грязным» квадратам начиная с

и их роли я относительно уверен, то вот какую роль и как играет квадрат от

(он же Фактор-9) сказать сложнее.
Опасаюсь делать серьезные выводы, так как не убежден, что точность моего компьютера позволяет эти выводы проверить на больших числах. А моделей может быть построено достаточно много.
Например, построю график, где Фактор-9 (в программе с ним связана литера «Т») начинает влиять с числа

(это

в квадрате) и будет «обнулять» каждую следующую

-ую нечетную точку. Привожу ниже график для такой модели. Изучить в подробностях можно, использовав программу GRAPH и соответствующий ей файл.
(ВСЕ ФАЙЛЫ ЕСТЬ)
График 2. Рис. 1. (немасштаб.) НАЧАЛО
с учетом Фактора-9 (

) – синяя линия,
и

распределения простых чисел – красная линия.
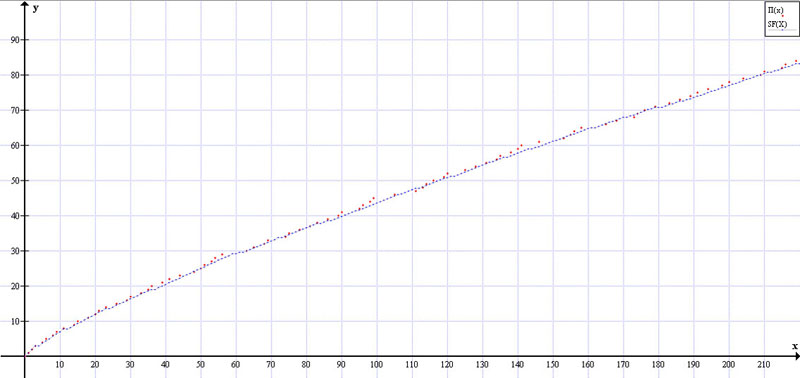 График 2. Рис. 2. (немасштаб.) ПРОДОЛЖЕНИЕ
График 2. Рис. 2. (немасштаб.) ПРОДОЛЖЕНИЕ
с учетом Фактора-9 (

) – синяя линия,
и

распределения простых чисел – красная линия.
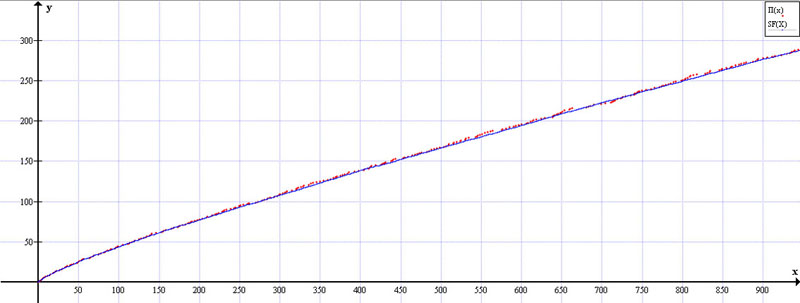 График 2. Рис. 3. (немасштаб.) ПРОДОЛЖЕНИЕ
График 2. Рис. 3. (немасштаб.) ПРОДОЛЖЕНИЕ
с учетом Фактора-9 (

) – синяя линия,
и

распределения простых чисел – красная линия.
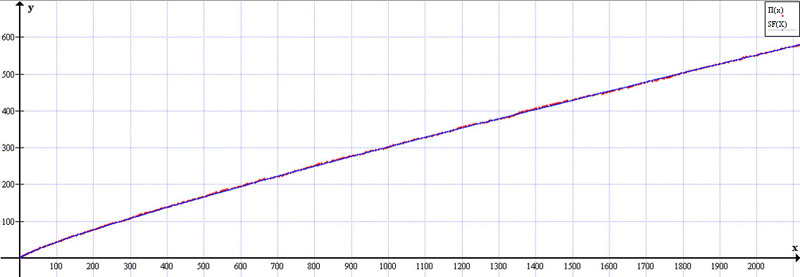 График 2. Рис. 4. (масштаб.) ВЕСЬ ИССЛЕДУЕМЫЙ ИНТЕРВАЛ
График 2. Рис. 4. (масштаб.) ВЕСЬ ИССЛЕДУЕМЫЙ ИНТЕРВАЛ
с учетом Фактора-9 (

) – синяя линия,
и

распределения простых чисел – красная линия.
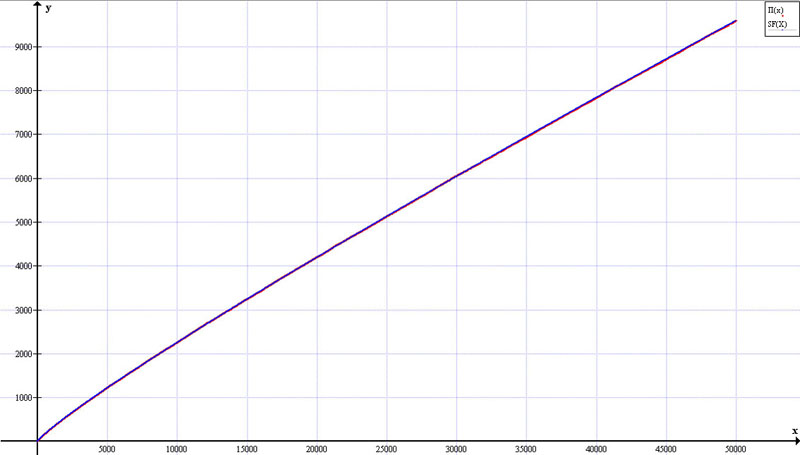
Итого, заданная таким способом для каждой нечетной точки числового ряда функция

приводит к получению

, которая в свою очередь практически полностью совпадает с

на всем исследуемом промежутке.


Игорь И.