Извините, что не ответил. Я вообще этого сообщения не заметил, так как тема вниз уехала по какой-то божественной причине.
Я вот что имел ввиду (сообразил, наконец). Пусть есть система линейной МНК-аппроксимации
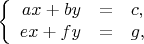
где

— угловой коэффициент прямой,

— свободный член (обозначения взяты для однообразия записи СЛАУ). Коэффициенты известно, как выражаются через результаты измерений.
Имеем тогда, например, для

решение

и относительную погрешность


Все эти дельты от коэффициентов в явном виде выражаются через ошибки измерений, соответственно и ошибка

тоже. Вот это я имел ввиду под погрешностью коэффициента.
не использовать ортогональные многочлены
А как использовать ортогональные многочлены? Ведь аппроксимация (наилучшая) имеет однозначный набор коэффициентов; как же их подогнать так, чтобы была ортогональность?



