rockclimberВот, уважаемый
amon подал хорошую мысль:
... можно сообразить откуда возьмется

-функция в пределе

Путём введения вспомогательного параметра

c последующим устремлением его к нулю можно немало понять про дельта-функцию даже без помощи википедии.
Правда, речь тут я веду о понимании лишь на "физико-техническом" уровне (т.е. о понимании, которому мы радуемся, пока математики не надерут нам уши за такое "понимание"). Мысль состоит в том, чтобы заменить исходную функцию

имеющую особенность в точке

сглаженной функцией

производные которой легко вычислить и при

Сглаженную функцию мы руками подберём так, чтобы

при

Кроме того, вместо общих выводов ограничимся рисунками с частными примерами; на языке рисунков производная это "наклон касательной" к графику функции (точнее: тангенс угла наклона), а определённый интеграл от функции одной пременной это площадь под графиком на определённом отрезке оси

(К заданию 1)
Рассматриваем функцию

. (Знак минус, заданный в заданиях
Munin-ом, для удобства не учитываю; ведь результат не сложно будет умножить на

чтобы приспособить его к

) График функции

похож на острый "зуб" пилы. Этот зуб можно сгладить многими способами. Начнём с самого простого:
а) Потребуем, чтобы на отрезке

график сглаженной функции

имел бы вид параболы, т.е. положим:

.
Коэффициенты

и

подберём так, чтобы в точке

(и в точке

тоже) парабола гладко сшивалась (стыковалась) с прямой, изображающей исходную функцию

при

(и при

) .
То есть, находим

и

из следующих двух условий, которые будут налагаться на

и в других наших примерах сглаживания:

Поскольку у нас

то получаем:

и

так что:

при

.
Теперь без проблем находим первую производную сглаженной функции:

при

,

при

,

при

.
В точках стыковки

график первой производной имеет изломы, но это не мешает нам найти вторую производную сглаженной функции всюду, кроме этих двух точек стыковки:

при

,

при

,

при

.
Посмотрим, как изменяются графики функций

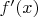
и

с уменьшением значений "параметра сглаживания"

Следует обратить внимание на то, что площадь под графиком

не зависит от
она равна

и значит, она будет равна

даже в пределе с

когда

превратится в




б) Второй пример из бесчисленного множества вариантов сглаживания - потребуем, чтобы при

сглаженная функция была "параболой" 4-ой степени:

Сшивая её, как и раньше, с исходной функцией

имеем в интервале


,

,

.
Опять-таки, площадь под графиком

не зависит от

и равна




в) В третьем примере сглаженная функция

выбрана так, что c
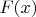
и

гладко "сшиваются" и она сама, и её первая производная соответственно:

при

.


В пределе с

все примеры дают одну и ту же картину:

Следует заметить, что "график"

здесь слегка условен; так, в примере (б) при любом конечном

в точке
вторая производная сглаженной функции равна нулю, но в пределе с

её боковые пики сближаются и вытягиваются вверх настолько, что мы вынуждены изобразить их в виде одного пика в точке

Площадь (интеграл) под графиком второй производной во всех примерах равна
В пределе с

все отличия конкретных примеров друг от друга, имеющиеся только на интервале

становятся несущественными, и это позволяет в таком пределе говорить об одной и той же функции (обобщённой):

.
Основное свойство дельта-функции

, как теперь видно, заключается в том, что интеграл от неё по любому интервалу, содержащему точку

равен единице:

.
(К заданию 2)
Ваше обозначение

заменим общепринятым:

где

имеет простую геометрическую интерпретацию - это расстояние в 3-мерном пространстве от начала координатной системы до точки с декартовыми координатами

Рассмотрим функцию

В начале координат она обращается в бесконечность. В шаре радиусом

(т.е. при

заменим её сглаженной функцией

, уже нигде не обращающейся в бесконечность:

при

,

при

.
В 3-мерном случае вместо одной производной у функции

появляются аж три частные производные: по

Они составляют векторное поле, называемое градиентом скалярного поля

и обозначаемое как

Например, как выясняется из величайших уравнений физики, - из уравнений Максвелла, - в задачах электродинамики функция

описывает поле электростатического потенциала, создаваемое точечным зарядом

находящимся в начале координат, а векторное поле

имеет смысл напряжённости электрического поля.
В нашем примере со сглаженной функцией

несложно вычислить декартовы компоненты векторного поля

т.е.

и найти его величину

т.е.:

.
Ответ получается такой:

при

,

при

.
Сумма вторых частных производных для

по

обозначается как

т.е.:

.
В нашем примере ответ для

получается такой:

при

,

при

.
Вот графическая иллюстрация этих ответов при разных значениях параметра



Интерпретация на языке электростатики здесь простая: наша функция

это потенциал заряда

равномерно размазанного по объёму шарика радиусом

В 3-мерной задаче термин "интеграл от скалярного поля" обычно означает
трёхкратное интегрирование - по переменным

что геометрически интерпретируется как интеграл по некоторому заданному объёму

Наглядно это означает, что значения подынтегральной функции умножаются на элементы объёма

внутри области

и суммируются.
В нашем примере очевидно, что вклад в интеграл по объёму от поля

может набираться только в шаре радиуса

с центром в начале координат, потому что только там

И поскольку там значения

постоянны, то их можно вынести из-под интеграла, так что интеграл по любому объёму

, заключающему в себе указанный шар будет равен значению

умноженному на объём шара


(по любому объёму

содержащему шар

) .
Как видим, правая сторона этого равенства не зависит от

Следовательно, это равенство сохраняется и в пределе с

когда

И значит, можно этот факт записать так:

,
где
3-мерная дельта-функция

определена своим интегральным свойством:

(по любому объёму, содержащему точку




