Как обычно, колебанием функции на множестве будем называть разность между максимумом (супремумом) и минимумом функции на множестве; колебанием функции в точке - предел колебаний функции на интервалах с центрами в точке, при стремлении к 0 длины интервала. Если в точке есть предел функции, то на примыкающих к этой точке интервалах колебания сколь угодно малы. Поехали: для любой точки

и для любого

построим интервал

, на котором колебание функции меньше

. Пусть
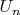
- их объединение по всем

. Множество
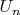
открыто и плотно. По Бэру (т.е., из принципа вложенных отрезков) , пересечение

всех
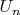
- плотно (и непусто, в частности). В точках из

функция непрерывна (колебание ее равно 0). Итого: если в каждой точке есть предел, то множество ее разрывов - первой категории.



