Кстати, может быть, Вам стоит так и попробовать запомнить для себя: если

мог бы быть любым, то ограничиваем его возможности знаком модуля (ибо нефиг!

), а вот если он не может быть отрицательным, то и знак модуля не нужен.
Хех, так сказать, "свобода — это осознанная необходимость". :)
arseniivСпасибо за совет. :) Звучит занятно.
Покрутил немного всякие функции в уме. Полагаю, дела обстоят так:
-
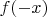 — зеркальное отражение графика функции
— зеркальное отражение графика функции  относительно оси ординат (т.е. отражение слева направо).
относительно оси ординат (т.е. отражение слева направо). -
 — зеркальное отражение графика функции
— зеркальное отражение графика функции  относительно оси абсцисс (т.е. отражение сверху вниз).
относительно оси абсцисс (т.е. отражение сверху вниз). -
 — график функции слева от оси ординат является зеркальным отражением графика справа от оси ординат.
— график функции слева от оси ординат является зеркальным отражением графика справа от оси ординат. -
 — на участках, где
— на участках, где  , график
, график  является зеркальным отражением графика
является зеркальным отражением графика  относительно оси абсцисс, а в остальном соответствует графику
относительно оси абсцисс, а в остальном соответствует графику  .
. -
 — сжатие графика вдоль оси абсцисс (относительно начала координат) в
— сжатие графика вдоль оси абсцисс (относительно начала координат) в  раз при
раз при  и растяжение в
и растяжение в  раз при
раз при  .
. -
 — растяжение графика вдоль оси ординат (относительно начала координат) в
— растяжение графика вдоль оси ординат (относительно начала координат) в  раз при
раз при  и сжатие в
и сжатие в  раз при
раз при  .
. -
 — сдвиг графика вдоль оси абсцисс вправо при
— сдвиг графика вдоль оси абсцисс вправо при  и влево при
и влево при  .
. -
 — сдвиг графика вдоль оси ординат вниз при
— сдвиг графика вдоль оси ординат вниз при  и вверх при
и вверх при  .
.
-- 20.03.2016, 14:46 --У моего планшета уже садился заряд, поэтому я был очень краток. :) Теперь могу ответить подробнее.
Пункт 2 и пункты с 5 по 8 мне уже в принципе знакомы, я и раньше имел о них представление. А вот пункты 1, 3 и 4 оказались интересны. :) И впрямь, всё выглядит проще, если представить это графически.
И кстати, вместо модуля в 3-4 можно взять ещё какие-нибудь периодические кусочно-линейные функции — например, дробную часть числа

, треугольную волну

(не пугайтесь записи, сначала нарисуйте график).
Я всё-таки предпочёл взять всякие функции попроще для мысленных экспериментов, а над Вашими ужасами я подумаю отдельно чуть позже. :) Никогда не имел дела с подобными зверушками, и не знаю, как с ними обращаться. Хотя смотрится интересно.
Насколько я понимаю, графиком

будет этакая "пила"? А графиком

будет та же "пила", но сдвинутая вниз на единицу?