Положительные рациональные числа

удовлетворяющие соотношение

(если такие числа существуют), должны удовлетворять неравенства

;

; (1)

; (2)
Если

, то

.

; (3)
Если

, то

.
Отметим, что из (2) следует (1), но не наоборот.

; (4)
Если
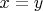
, то

, откуда следует, что
![$\sqrt[3]{2}=\frac{z}{x}$ $\sqrt[3]{2}=\frac{z}{x}$](https://dxdy-04.korotkov.co.uk/f/f/2/6/f265fd7bf5a5e609b74db7dabb17fbd282.png)
, где

и

- рациональные числа, но число
![$\sqrt[3]{2}$ $\sqrt[3]{2}$](https://dxdy-03.korotkov.co.uk/f/e/0/d/e0db901a13e9b18861b1a7edb00bdf4a82.png)
иррациональное.
Условия (2), (3), (4) позволяют сделать вывод, что числа

могут быть выражены сторонами разностороннего остроугольного треугольника. Наибольший угол

этого треугольника, лежащий против стороны

, удовлетворяет неравенству

Если

то сумма углов треугольника была бы меньше

.
Тогда

,

.
Обозначим

.
По теореме косинусов

, или

.
Так как

- рациональные числа то и

- рациональное число. Разделим на
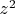
и получим

.
Обозначим

;





, где

- рациональное число.
Имеем систему

Ее решение –

;

.
Где

– рациональное число, которое без потери общности можно считать равным 1. Рациональное число

запишем как отношение натуральных чисел

В результате

;

;

,

,

.
Так как

получаем следующее:

,

,

.
Из условия

имеем




Из условия

имеем



Решаем неравенство, относительно



Следовательно, или

;

, что невозможно, ибо

.
или

;

.
Таким образом

удовлетворяет двойное неравенство

Предположим существование таких значений как

, что определяемые ими

удовлетворяют уравнение

.
Зафиксируем необходимые значения и их и рассмотрим.
Две непрерывные функции от

на интервале

;


;

.
Для выполнения равенства

, необходимо, что бы нашлось натуральное число

, такое что

и



Производные от которых


на промежутке

Обе функции монотонно возрастают на промежутке, при этом на его концах значения первой функции меньше соответствующих значений второй. Следовательно, ни при каком значении

из этого промежутка не будет выполняться равенство

и так же равенство

. Таким образом, это уравнение не имеет положительных рациональных решений (в том числе натуральных). Эти рассуждения можно привести для любого показателя степени n, такого что

.
Рассмотрим уравнение

.
Положительные рациональные числа ему удовлетворяющие должны удовлетворять неравенству

(5)
Отметим, что из (5) следует (2) и (1), но не наоборот.
Проведя полностью аналогичные предыдущим рассуждения, приходим к выводу, что уравнение

не имеет рациональных положительных решений и что это справедливо для любого показателя степени n, такого что

.
Повторяя эти шаги для

, приходим к выводу - уравнение

при ЛЮБОМ

не имеет положительных рациональных решений (в том числе и натуральных). Ограничимся пока натуральными значениями
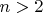
. Если

– четное число, то очевидно, что уравнение

не будет иметь никаких рациональных решений.
Если

– нечетное, то

не могут быть одновременно отрицательными рациональными числами, так как умножение уравнения на
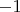
приведет к положительным рациональным решениям.
Очевидно, что невозможны случаи
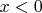
;

;

и

;
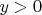
;

.
Рассмотрим возможность
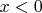
;
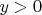
;

:



При этом
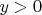
;

;

, т.е. уравнение имеет положительные рациональные решения, что невозможно.
Возможность решения при

;

;

рассматривается аналогичным образом.
Рассмотрим возможность решения при
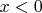
;
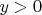
;

:


при этом
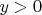
;

;

что невозможно.
Аналогично

;

;

.
Рассмотрим случай

.
Имеем уравнение

из которого вытекает, что
![$(\sqrt[m]{x})^e+(\sqrt[m]{y})^e=(\sqrt[m]{z})^e$ $(\sqrt[m]{x})^e+(\sqrt[m]{y})^e=(\sqrt[m]{z})^e$](https://dxdy-02.korotkov.co.uk/f/5/2/e/52ee979d19f07533b7dcd249c42b75fb82.png)
Для существования рациональных решений все радикалы должны иметь рациональные значения.
Приходим к уже рассмотренным возможностям.
В случае иррационального показателя степени n предельным переходом приходим к тому же выводу:
"Уравнение

, при любом
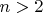
;

", имеет решением такую тройку чисел, что по меньшей мере одно из них является иррациональным. Например, уравнение

имеет решение
![$x=1; y=2; z=\sqrt[3]{9}$ $x=1; y=2; z=\sqrt[3]{9}$](https://dxdy-03.korotkov.co.uk/f/6/9/1/691db76b2858263e9a987db5673744d582.png)
"
В общем, как то так. Доказательство не мое, я всего лишь рерайтер. Так что возможны мелкие или же крупные ошибки, которые, надеюсь, опытные форумчане, а так же, уважаемые модераторы, выявят. Автор сего труда, Желтков В.Ю., мой непосредственный родственник,так что конструктивные замечания и или же указания на ошибки не останутся незамеченными.
Всем спасибо.



