Xaositect, Ну тогда неопределенный интеграл равен

Можно продифференцировать обратно и убедиться что это так. Возьмем к примеру,

,



Второе слагаемое,

, всегда конечно и стремится к

, т.к.

стремиться к бесконечности, то и любая его положительная степень, в данном случае - по сути, корень

-й степени, (умноженная на константу, в данном случае
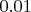
) будет стремиться к бесконечности. А

деленное на число стремящееся к бесконечности, будет стремиться к

.
Значит, формула сильно упрощается, нужно рассматривать только первое слагаемое, и этот несобственный интеграл, вообще говоря, зависит только от

.

При

стремящемся к

,

будет стремиться к

, а потому, формула для интеграла еще больше упрощается, точнее, значение интеграла
эквивалентно равно

Я даже не ожидал, что настолько упростится вычисление этого интеграла. Ну тогда всё понятно, при

это значение интеграла равно бесконечности, потому и сумма ряда

по всем натуральным

от

до

, расходится и бесконечна. (мы получили второй вариант доказательства этого). Этот ряд расходится еще медленнее чем гармонический.
Трудно придумать еще медленнее расходящийся ряд. Но стоит добавить к степени

, сколь угодно малое

,и неважно, для множителя

, или

, и ряд уже перестает расходиться, к примеру, для любого

этот ряд сходится, и сумма его конечна -

.
Спасибо за помощь, с этой задачей было интересно разобраться! :) Изучил самые медленно расходящиеся ряды.
-- Чт мар 17, 2016 20:43:33 --Надеюсь, нигде не ошибся.