Никак не могу понять одну вещь. Уже целый месяц возвращаюсь к этому вопросу - и все безрезультатно.
Возьмем банахово пространство

непрерывных функций, исчезающих на бесокнечности. То есть

Пусть топология будет стандартной, индуцированной супремум-нормой:

Пусть для простоты

Очевидно, что пространство функций с компактным носителем

плотно в

Рассмотрим теперь слабую* топологию на двойственном пространстве

Пусть мы индуцируем эту тополгию с помощью полунорм вида

Очевидно, что в этой топологии все функционалы вида

непрерывны при

рассмотрим теперь такой функционал, только допустим, что

лежит в

Известна теорема, что линейный функционал

непрерывен в локально выпуклой топологии на векторном пространсве

(индуцированной семейством полунорм

) тогда и только тогда, когда существует полунорма

для которой действительно:

где

То есть как будто бы функционал

не должен быть непрерывным. Ведь какую бы мы ни взяли функцию

мы можем взять, к примеру, функционал

и тогда вышеуказанное неравенство не выполняется. А значит функционал

не непрерывен на

С другой стороны, пусть дана любая сходящаяся к

последовательность

в слабой* топологии на

И пусть последовательность

сильно ограничена. То есть

Теперь рассмотрим выражение

Если оно истинно, то функционал

непрерывен в слабой* топологии.
Мы знаем, что

по определению слабой* топологии истинно для

Пусть

сходящаяся к

последовательность функций из

Рассмотрим теперь выражение (учтем, что

)

Так как все

равномерно ограничены константой
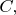
а

равномерно сходится к нулю, то после предельного перехода по

мы получаем, что

То есть

непрерывен в слабой* топологии на

и мы получили противоречие.
--------
Как быть? Где моя ошибка?



