Здравствуйте, уважаемые форумчане.
Задача: Окружность, вписанная в равнобедренный треугольник

, касается основания

в точке

и боковой стороны

в точке

. Точка

-- середина стороны

, а точка

точка пересечения окружности и отрезка

, отличная от

. Касательная к окружности, проходящая через точку

, пересекает сторону

в точке

. Найти угол

, если известно, что

.
Обозначения:



Что удалось выяснить:

, поскольку средняя линия, откуда треугольник
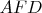
- равнобедренный.

, как внешний для треугольника
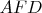
.
По теореме о секущей и касательной для

и

, но

, тогда

Высота по теореме Пифагора:

, тогда по теореме косинусов

. (треугольник

).
Еще

, как касательные проведенные из одной точки, то есть

.

, как касательные проведенные из одной точки.
Можно еще из треугольника

выразить

, но этого всё равно не достаточно.
Если было бы известно, в каком отношении касательная (которая проходит через точку

) делит отрезок

- можно было бы использовать теорему Менелая для треугольника

.
Как быть?
off: рисунок
(Оффтоп)



