Не очень ясно, что значит "из верхней полуплоскости" при

, например
С

проблем нет, корни

и в верхней полуплоскости только один. А для

верно заметили. Тогда положим сразу по определению
![$\sqrt[2^n] 1 = 1$ $\sqrt[2^n] 1 = 1$](https://dxdy-04.korotkov.co.uk/f/b/8/b/b8b17ff044e7e5e4a871c7c62ecde69b82.png)
.
Ну а так-то у нас аргумент по формуле Муавра на каждой итерации кроме, быть может, первой, вдвое уменьшается, а модуль остаётся неизменным.
Вообще, я пытаюсь аксиоматически определить тригонометрические функции

и

как компоненты непрерывного нетривиального гомоморфизма из группы
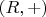
в ортогональную группу вращений

или, что то же самое, в группу комплексных чисел с модулем

по умножению. Поэтому нельзя опираться на формулу Муавра и тригонометрические функции.