Мысли вслух. Требуем чтобы предел был

. Если

, тогда

. Если

, тогда

. Значит

.
Спасибо.
А что такое порядок роста?

Я руководствовался
этим определением.
Я должен представить себе это дело графически?
Я думаю, что графически представлять не нужно.
Charlz_Klug
Нормально, только зачем вам предел? Пользуйтесь эквивалентностью!
Я рассудил так: поскольку эквивалентности определены для условия

, а у меня

, то следует привести некую
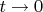
.
Ну.. можно просто "по сравнению с

". Постоянный множитель роли не играет.
Спасибо.



