Все треугольники с рациональными длинами сторон

и рациональной площадью равной периметру задаются 2-параметрически:

, где

- рациональные числа. При этом площадь

.
(отсюда следует, например, что длины сторон в таких треугольниках больше 4).
Т.о. уравнение

определяет сингулярные числа

. Как выше было замечено

.
Последовательность сингулярных чисел выглядит так:

Она получается из рассмотрения надлежащим образом подобранной эллиптической кривой,
например,

.
Интересно, что при
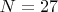
имеется только один соответствющий треугольник со сторонами

.
Для остальных

из приведенной последовательности кол-во треугольников бесконечно. Это связано с количеством точек кручения на кривых

и рангом этих кривых.
А именно:

точек кручения при
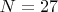
(ранг кривой равен нулю) и

точки кручения при

и ранги кривых больше нуля.
Отрезок

совпадает с отрезком последовательности A135412 из OEIS.