Здравствуйте! Попалась задача, указание к которой наоборот усложняет решение. Я склоняюсь к тому, что ошибка все-таки где-то в моем решении без использования этого указания, да к тому же в моем решении не используется часть условия. Скорее всего, косяк у меня, а найти не могу. Помогите, пожалуйста. Итак, задача.
Пусть порядки групп

и

взаимно просты. Докажите, что каждая подгруппа группы

имеет вид

, где

,

. Отношение

значит "быть подгруппой".
Решение. Вот указание: Проверьте, что если

, то найдутся такие

и

, что

,

.
Проверяю. В том сборнике знак

обозначает порядок группы или элемента. Итак, беру этот элемент

. Тогда

делит
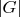
,

делит

. Но

, поэтому

. Значит, существуют такие целые

и

, что

, откуда

. Значит,

Значит, если

, то и

. Точно также докажу, что

. Пусть теперь

- некоторое подгруппа

, и

тогда


. Применяя рассуждения, аналогичные приведенным выше, получу, что

Т.к.

- подгруппа, то в нее входит


откуда


С другой стороны, например,

отсюда


Этим, как будто можно считать утверждение доказанным, да вот беда: непонятно, зачем вообще переходить к элементам с единицами? ИМХО, утверждение прекрасно доказывается сразу, только при этом непонятно, как использовать указание к задаче, а взаимная простота порядков групп вообще не применяется. Или я где-то ошибся?



