Свойства нечетного ряда чисел (1) были известны еще греческому математику Никомаху (около 100 г. н.э.). Труды же математиков тех времен интересовали Ферма. Особенно он уделял внимание Диофанту, который мог быть и современником Никомаха, так как промежуток времени, когда мог жить Диофант, перекрывает время жизни Никомаха. Да и "Введение в арифметику" Никомаха было учебником на протяжении практически тысячи лет. Чтобы понять хотя бы немного логику Ферма и необходимо работать с материалом, на котором делал свои выводы Знаменитый Француз.
Итак, посмотрим какие же ограничения для существования решений УФ могут дать свойства нечетных чисел:
1.Последовательности нечетных чисел, суммы которых образуют кубы, непрерывно вписываются в ряд нечетных , но не перекрывают друг друга (1). Это легко объяснимо.

. То есть имеем

чисел со средним значением

.Поэтому всегда можно найти различные числа, набор которых будет удовлетворять условию среднего значения. Этому же условию удовлетворяют и нечетные числа арифметической прогрессии с начальным

и последним

числами. Не трудно убедиться , что сумма этой прогрессии
![$$\frac{[x^2-(x-1)+ x^2+(x-1)]x}{2}=x^3$$ $$\frac{[x^2-(x-1)+ x^2+(x-1)]x}{2}=x^3$$](https://dxdy-03.korotkov.co.uk/f/a/6/6/a66671823ca051c2f3df9e90b429899d82.png)
А разность в соседних последовательностях между начальным числом второй и последним нечетным первой и
![$[x^2-(x-1)]-[(x-1)^2+((x-1)-1)]=2$ $[x^2-(x-1)]-[(x-1)^2+((x-1)-1)]=2$](https://dxdy-04.korotkov.co.uk/f/f/d/f/fdff5236fa91903b89cacc47572d1b3682.png)
. Что и соответствует непрерывному ряду нечетных.
2. Квадраты не имеют подобного свойства. Действительно

. Среднее значение

. Первое число арифметической прогрессии

. Таким образом, все квадраты образуются суммой последовательности нечетных чисел, начинающихся с 1. Здесь необходимо напомнить, что мы рассматриваем только вариант, когда количество нечетных в последовательности равно основанию степени.
3. Другие степени

. Разность в соседних последовательностях между начальным числом второй и последним нечетным первой
![$[x^{p-1}-(x-1)]-[(x-1)^{p-1}+(x-1-1)]>2$ $[x^{p-1}-(x-1)]-[(x-1)^{p-1}+(x-1-1)]>2$](https://dxdy-02.korotkov.co.uk/f/9/0/a/90aaa0b9931d64c250702d22e4a6422782.png)
Поэтому при
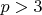
соседние последовательности имеют между собой не задействованные нечетные числа ряда.
4. Понятно, что составное с числами разной четности

не может быть представлено суммой последовательности нечетных с количеством чисел в последовательности

или

. Поэтому арифметическая прогрессия последовательностей натурального ряда не может быть преобразована в последовательность нечетных с тем же количеством чисел.
5. Последовательности нечетных, суммы которых образуют разности соседних кубов, не имеют свойства последовательностей кубов по непрерывному заполнению нечетного ряда. Действительно, разности соседних кубов могут быть простым числом, которое (как уже сообщалось) не возможно представить суммой последовательности нечетных. Разности соседних кубов могут быть также квадратами, последовательности нечетных для которых всегда начинаются с 1. Поэтому заполнение нечетного ряда будет происходить либо с не задействованными числами ряда между соседними последовательностями, либо они будут иметь общие нечетные числа.