< Геометрическое определение векторов и свойства операций над ними. >
Установив эти наглядно-геометрические, интуитивные факты, мы можем теперь обратить точку зрения и принять их за аксиомы.
< Аксиоматическое алгебраическое определение векторов. >
Подчеркнем, что это определение не накладывает никаких ограничений на природу элементов линейного пространства (векторов) и на конкретное воплощение операций сложения и умножения на число. Поэтому могут существовать (и действительно существуют) много различных линейных пространств.
< Далее следуют примеры, включая
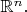
>