Ну конечно то что у Вас на картинке , можно и с любым связным графом проделать, пока не превратится в дерево. Берем любой цикл и разрываем его, так как это был цикл, связность не нарушится. Все кончится деревом, с поправкой, что некоторые висячие вершины дерева "выколотые".
Я пока не увидел тут "олимпиадной задачи", а просто обсуждение всего вообще.
Тогда, может быть, нужно отдалиться от графов и попробовать найти другие такие множества в
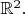
Например, кажется, что
это можно сделать со скатертью Серпинского
kp9r4d, прошу прощения!

Я имел в виду следующее:
 Munin
Munin, не совсем понимаю, что именно нарушается. Я сейчас не рассматриваю граф в привычном смысле. Сейчас это определённые кривые в
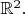
Хмм... А как Вы введёте структуру CW-комплекса для графа, у которого в единственной вершине счётное количество вложенных друг в друга петель и больше ничего?
-- 01.10.2015, 18:11 --Ааа, я понял.
Munin, Вы правы. Просто, как я уже написал выше, давайте прекратим рассматривать графы, так как это сбивает с толку. Например, если рассмотреть конструкцию "в единственной вершине счётное количество вложенных друг в друга петель" в

, то она вроде как не будет эквивалентна никакому CW-комплексу. В смысле гомотопически.



