"В космосе без отталкивания" у гравицапы не получилось изменить орбиту сутника "Юбилейный".
Интересно, на каком принципе эта гравицапа была основана? Может, что-то вроде этого:
...возможны двигательные системы, работающие за счет неоднородностей гравитационного поля, которые для перемещения полезного груза в поле тяжести вообще не нуждаются в бортовых запасах массы.
Принцип их работы основан на использовании так называемых приливных сил (рис. 14). Если две массы, связанные тросом, вращаются на орбите искусственного спутника Земли, то в целом такая система движется со скоростью, соответствующей орбите ее центра масс. В результате масса, наиболее удаленная от Земли, будет иметь большую скорость, чем нужно для ее равновесного движения, и поэтому на нее должна действовать избыточная центробежная сила. Для ближней к Земле массе, наоборот, скорость меньше равновесной и имеется избыточная гравитационная сила, равная и противоположно направленная сила, приложенной к верхней массе.
Эти силы называются приливными. Они натягивают трос, и, распуская трос с трением, мы заставим приливные силы совершать работу. Эта работа осуществляется за счет кинетической энергии системы, и в итоге центр тяжести ее будет переходить на более низкую орбиту. Подобным же образом приливные силы, действующие между планетами, вызывают их взаимное сближение. Например, океанские приливы, вызываемые Луной, в результате трения о поверхность Земли приводят к уменьшению расстояния между Луной и Землей.
И, наоборот, совершая работу против действия приливных сил, можно повысить орбиту центра тяжести системы. Для повторения цикла после полного сближения масс их нужно оттолкнуть при свободно распускающемся тросе. Но эффективность такой двигательной системы в околоземном пространстве очень мала.
Величина приливных сил равна произведению ускорения силы тяжести на орбите на отношение расстояния между массами к радиусу орбиты. На орбите высотой

км при расстоянии между массами

км она составляет

Н/кг, на геостанционарной орбите —

Н/кг. Работа, совершаемая за один цикл сближения, соответственно равна

и

Дж/кг. Чтобы перевести космический аппарат с орбиты высотой

км на геостационарную орбиту (

км), потребуется около

циклов. Даже если допустить, что каждый цикл будет совершаться за

с, то на такое перемещение потребуется более

лет.
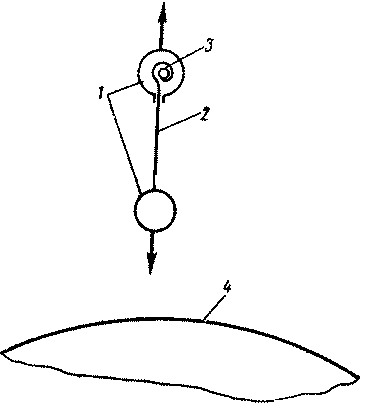 Рис. 14. Схема «гравитационного» двигателя (стрелками указано направление приливных сил): 1 — полезный груз, 2 — трос, 3 — устройства для намотки троса, 4 — Земля
Рис. 14. Схема «гравитационного» двигателя (стрелками указано направление приливных сил): 1 — полезный груз, 2 — трос, 3 — устройства для намотки троса, 4 — Земля