L^infinity, positive measure

[Bridgeport]

If \mu is a positive measure, each f \in L^{\infty} defines a multiplication operator M_f on L^2(\mu) into L^2(\mu), s.t. M_f(g)=fg. For which measure \mu is it true that \|M_f\|=\|f\|_{\infty} for all f \in L^{\infty}(\mu)?
For which f \in L^{\infty(\mu), M_f maps L^2(\mu)onto L^2(\mu)?

[Dan B-Yallay]

Bridgeport писал(а):

Let f \in L^{\infty}(\mu). Define multiplication operator M_f:L^2(\mu)\rightarrow L^2(\mu) by M_f g= fg.

First of: what is $L^{\infty}(\mu)$? It is usual to put some space or set instead of $\mu$ but in your case it seems that you're talking about measure.

Bridgeport писал(а):

Question: for which measure \mu is it true that \|M_f\|=\|f\|_{\infty}?
for which f \in L^{\infty(\mu), M_f maps L^2(\mu)onto L^2(\mu)?

Try to check what happens if $f=0$ on some set of positive measure.

[Henrylee]

I guess, $\mu$ - is a probability measure, right?

[Bridgeport]

To answer some questions:

The above problem is from Rudin "Real and Complex analysis". I guess for the space we can take \mathbb R. L^{\infty} - space of functions bounded a.e.

I do not see how probabilitiy measure would work.(the question is to find the measure)


I found trivial answer to the first question:\mu=0. The second question I think now is easy f=1.

Any non-trivial solutions?

P.S I just edited original message. I added in the first question: for all f \in L^{\infty}(\mu)?

Добавлено спустя 19 минут 32 секунды:

Now I see that suggestion to try f=0 is similar to trivial solution\mu=0 ( after fixing initial typos.)

Sorry for so much confusion!

[Dan B-Yallay]

Bridgeport писал(а):

I found trivial answer to the first question: $\mu=0$. The second question I think now is easy $f=1$.

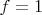
Any non-trivial solutions?.....

P.S I just edited original message. I added in the first question: for all $f \in L^{\infty}(\mu)$?

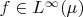
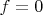
Now I see that suggestion to try $f=0$ is similar to trivial solution$\mu=0$ ( after fixing initial typos.)

Sorry for so much confusion!

Well, the problem actually is not that easy.
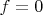
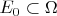
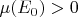
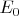
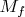
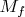
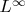
I was not suggesting that you take $f=0$ on whole domain, say $\Omega$. Only on some subset $E_0 \subset \Omega$ with $\mu(E_0)>0$. Then all functions that have $E_0$ as support will be mapped into zero. Which means they are not in the range of $M_f$ and therefore, $M_f$ is not ONTO. So throw such an $f$ from $L^{\infty}$ because it does not satisfy the requirement.

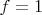
You were right about $f=1$ but it's just a particular case.
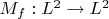
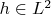
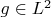
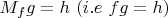
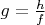
My main idea was: by definition the map $M_f: L^2 \rightarrow L^2$ is onto, if for any $h \in L^2$ there is a preimage $g \in L^2$ such that $M_f g = h \ (i.e \ fg =h)$. But as long as $f$ stays away from zero on it's domain, you can always solve that equation for $g$ just by dividing both sides by $f$ i.e. $g= \frac h f$. However this is sufficient condition. May be not necessary. Try to play with the rest.

Bridgeport писал(а):

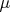
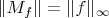
Question: for which measure $\mu$ is it true that $\|M_f\|=\|f\|_{\infty}$ for all $f \in L^{\infty}(\mu)$?

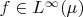
Not sure what is being asked here. I couldn't find this problem in my Rudin's book. Perhaps different edition, I guess.
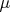
Anyway, the solution $\mu = 0$ seems wrong. We need to figure for which set function $\mu$ the following is true:

$$ \|M_f\|_{L_2}= \mathop {\sup }\limits_{g \in L^2, \|g\| \le 1} \sqrt{\int_{\Omega} |fg|^2 d{\mu}} = ess \mathop {\sup }\limits_{\Omega} |f| = \|f\|_{L^{\infty}} $$

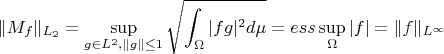
for all $f \in L^2$

It is hard to answer without knowing the context of the problem.

[Bridgeport]

I now edited the original post so that it is exactly as in Rudin's book.

Thank you for clarifications regarding onto part.

Still, it looks like trivial measure would work for the second part. Under trivial measure everything is zero.