По-моему, все-таки приближенным. Кажется, это называется параболическим приближением, когда пренебрегают второй производной.
Да, именно так. Гауссов пучок - приближённое решение классического волнового уравнения. Ссылки на книжки не привожу; кому необходимо, тот сам легко нагулит, а краткий вывод формулы для гауссова пучка опишу (бумажка с выводом у меня как раз перед глазами на столе валяется: намедни как раз проверял эту формулу перед численным счётом).
Решение

классического волнового уравнения

ищем в виде:

,
где

Такое решение описывает "плоскую волну", распространяющуюся вдоль оси
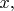
с амплитудной "огибающей"

Мы хотим найти решение, у которого огибающая убывала бы с расстоянием довольно быстро в поперечных направлениях

"узкий пучок") и при этом почти не менялась бы в продольном направлении (
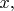
"почти не расходящийся пучок"). Длина волны считается малой по сравнению с интересующими нас расстояниями, так что волновое число

- большая величина. Подстановка указанной функции

в волновое уравнение ведёт к уравнению для огибающей:

.
И вот тут (внимание!) мы переходим к приближённому уравнению - отбрасываем член

Т.е. далее мы ищем точное решение, но уже приближённого уравнения:

.
Переписав его в виде

,
замечаем полное сходство с "волновым уравнением Шрёдингера" квантовой механики для частицы с величиной

в роли массы

совершающей свободное 2-мерное движение в плоскости

но только здесь роль времени

играет переменная
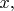
а постоянная Планка
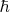
равна единице:

.
Хорошо известно (и легко проверяется), что частные решения этого уравнения КМ имеют вид бегущих плоских волн:

,
а общее решение можно представить суперпозицией таких частных решений с произвольными (в меру произвольности начальных условий) коэффициентами

(где

и

- двумерные векторы с y- и z-компонентами):

.
Коэффициенты

можно задать как коэффициенты Фурье для начальной волновой функции


.
Подставим сюда "гауссовский колокол"

где
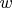
- параметр ширины,

- произвольная амплитуда. Каждый из двух имеющихся в

однократных интегралов с бесконечными пределами по

и

элементарно "берётся" с помощью известной формулы

так что для

получается тоже гауссова экспонента - с квадратичным по

показателем. Поэтому с помощью той же формулы

элементарно вычисляется двукратный интеграл для

по

и

с бесконечными пределами; в итоге имеем:

.
В КМ это одно из точных решений 2-мерного нестационарного ("волнового") уравнения Шредингера; такая волновая функция описывает неподвижный гауссов волновой пакет, расплывающийся с течением времени

А в волновой оптике эта функция (с заменой

на

и

на

имеет смысл огибающей

в приближённом решении 3-мерного классического волнового уравнения. Такого типа решение и называют гауссовским пучком:

.
Заодно поясню, по каким формулам строились приведённые выше картинки гауссовских пучков. Сначала каждый множитель в комплексном решении

надо представить в виде

тогда вся функция

тоже запишется в показательной форме:

.
Затем переходим к вещественному решению взятием действительной части от этой комплексной функции; и, кроме того, полагаем
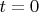
и


.
Если для краткости обозначить

и

то имеем:

, где:

.
Теперь у нас

означает радиус-вектор произвольной точки в плоскости с декартовыми координатами

Чтобы получить формулу для повёрнутого пучка, т.е. для пучка, подвергнутого действию оператора поворота

пользуемся стандартным (и довольно очевидным) правилом преобразования скалярного поля:

.
Так, чтобы повернуть конфигурацию

вокруг оси

на угол

против часовой стрелки, сначала выписываем выражения для компонент радиус-вектора

повёрнутого на угол

по часовой стрелке:

,

,
и затем подставляем эти выражения соответственно на место переменных

и

в

Получившееся выражение будет описывать функцию

Аналогично, для сдвига полевой конфигурации на какую-либо величину
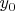
вдоль оси

надо заменить в формуле поля переменную

на переменную




