Рассмотрим тройки

и

.
Справедливы тождества:




.
Все правые части, кроме первой строки - квадраты.
Рассмотрим Уравнение

Полагая

получаем уравнение эллиптической кривой

Оно записывается в форме Вейерштрасса

с помощью замены переменныx

. На кривой

имеется рациональная точка

.
На кривой

ей соответствует рациональная точка

. Из теоремы Лутц-Нагель

- точка бесконечного порядка
(поскольку она имеет дробные координаты).Таким образом, на кривой

, а сл-но и на кривой

бесконечно много рациональных точек. Числители и знаменатели x-координат этих точек - это
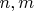
Они и обеспечивают бесконечное кол-во необходимх троек.
Точке

соответствует пример, приведенный ТС.
Точке

соответствует тройка еще более внушительная

. И так далее.



