Рассмотрим т.н. фукнцию Уиттекера

определяемую как одно из (двух независимых) решений уравнения:

Меня интересует случай когда

, а

, где

и
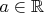
. Другими словами,

- чисто действительное число, а

- чисто мнимое. Можно показать, что при указанных предположениях относительно индексов функции Уиттекера она является чисто вещественной.
Рассмотрим решения

уравнения

. В статье Л.А. Дикого "О корнях функции Уиттекера и функции Макдональда комлексного индекса" 1960 года показывается что в этом случае корней функции Уиттекера счетно много и все они расположены на лучше

, т.е., все корни неотрицательны, и более того их концентрация растет по мере приближения к началу координат справа. В работе Дикого также показывается, что корни функции Уиттекера непрерывно зависят от ее индексов. Отсюда можно сделать вывод, что для любого

, найдется

такое что

.
Меня интересует вопрос монотонности: Пусть
![$0\le x_1<x_2$. Рассмотрим уравнение [math]$W_{\varkappa,i a}(x)=0$ $0\le x_1<x_2$. Рассмотрим уравнение [math]$W_{\varkappa,i a}(x)=0$](https://dxdy-02.korotkov.co.uk/f/5/8/2/582b07a0d2798f2dbeb723bbadcbbc9c82.png)
как уравнение на

при фискированных

и

. Пытаюсь показать что

.
Основная идея-использовать теорему о сравнении Штурма: если

,

, и

для всех
![$x\in[A,B]$ $x\in[A,B]$](https://dxdy-01.korotkov.co.uk/f/0/2/5/0252433c951e1a12fd06edaf0c05c4b682.png)
, то нули

не перемежаются с нулями

, и если

два последовательных нуля

то между ними находится как минимум один нуль

.
В случае уравнения Уиттекера роль функций

и

играет функция

которая является действительной при чисто мнимом

, и возрастает с ростом

. Достаточно ли этого?



