Пока народ ищет ссылки...
Криволинейный интеграл второго рода

не зависит от пути интегрирования, если

, что у Вас выполнено. Вот и зададим функцию

в точке
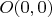
произвольно, а в любой другой точке

так:

Остаётся проверить, что она удовлетворяет условиям. Построим прямоугольник с вершинами

. Тогда

с точностью до постоянного слагаемого

равна любому из выражений


Первое выражение удобно для проверки

, второе — для проверки

.
Дальше начинаются вопросы, вроде «а что делать, если не весь прямоугольник принадлежит области?», но я своё дело сделал — показал идею.



