Здравствуйте, уважаемые форумчане!
Столкнулся со следующей задачей:
нужно найти наибольшее значение параметра

, при котором система уравнений

имеет бесконечное количество решений.
Вот что я делаю:
из перовго уравнения

подставляем во второе и получаем:

или окончательно для
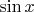

Поскольку

, то имеем

Решение:

и
 -- 23.05.2015, 14:25 --
-- 23.05.2015, 14:25 --Получается, что

, но правильный ответ другой (проверял на wolframalpha)
Где я что-то упустил?