Это, конечно, не верно. Но его можно использовать при доказательстве равенства мультипликативных норм матриц
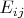
и

.
В смысле можно было бы использовать, если бы оно было верно?
В данном случае используется тот факт, что преобразованием подобия матрицу
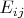
можно привести к матрице

и наоборот.
Отсюда, применяя свойства мультипликативной нормы, получаем, что

.
-- Ср май 20, 2015 00:52:44 --Собственно, вы зря Narn не послушали. В том тексте из леммы 11 сразу следует, что существует матричная норма, такая что эта норма
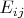
сколь угодно мала (если
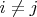
).
Я начал читать лекции, на которые дал ссылку
Narn. Нашел там кучу опечаток. Такое подозрение, что и в
лемму 11 закралась какая-то ошибка. Надо внимательно разобрать ее доказательство.