Да, похоже, я упустил из виду нормальную компоненту силы натяжения, возникающую из-за изменения направления последней.
-- Пн апр 27, 2015 20:16:45 --Постараюсь исправиться. Допустим, мы имеем дело с установившимся режимом, когда цепь движется вдоль некоторой фиксированной плоской кривой с постоянной скоростью

. Пусть уравнение этой кривой имеет вид

, тогда тангенс угла наклона касательной к этой кривой

Рассмотрим силы, действующие на движущийся элемент цепи длиной, равной расстоянию, проходимому цепью за время

, находящийся в точке

. Его масса равна

, где

- погонная масса цепи. На него с двух сторон действуют силы натяжения

и

, а также сила тяжести

. Поскольку его скорость неизменна по модулю, проекция суммарной силы на касательную к траектории равна нулю:

,

(скорость изменения абсолютной величины силы натяжения, действующей на наш элемент, по мере его движения)
Теперь запишем выражения для ускорений этого элемента вдоль координатных осей:


Что дальше делать со всем этим добром, непонятно.

Видимо, следует попытаться воспользоваться информацией, любезно предоставленной
Oleg Zubelevich, о том, что траектория в действительности представляет собой цепную линию.
Впрочем,

и

тривиально интегрируются:


Если за момент времени

принять момент прохождения элементом высшей точки траектории, то
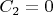
. Тогда из

и

следует:


С учётом того, что

,


Отсюда

(примем, что при


)

Таким образом,

Параметр

можно найти, например, из

, зная натяжение в верхней точке траектории. В свою очередь, натяжение в нижней части траектории - это сила, придающая импульс, соответствующий скорости

, вытягиваемым из кучи звеньям цепи.