Отсутствие периодических траекторий

[scwec]

На $\mathbb{R}^3$ заданы три гладких векторных поля всюду линейно независимых. Их линейные комбинации с вещественными коэффициентами порождают Алгебру Ли $g^3$, имеющую одномерный идеал $g^1\subset{g^3}$.
Пусть поле $X\in{g^1}$, а у присоединенного эндоморфизма $ad_X$ имеется хотя бы одно ненулевое вещественное собственное значение.
Докажите, что ни у одного поля из $g^3$ нет периодических траекторий.

[scwec]

Выберем в качества базиса $g^3$ поля $X_1=X\in{g^1}$, $X_2$ произвольное поле из $g^3$ неколлинеарное $X_1$, а $X_3\in{g^3}$ произвольное, но такое, чтобы $X_1,X_2,X_3$ были линейно независимы.
1-формы $\omega^1,\omega^2,\omega^3$ таковы, что $\omega^i(X_j)=\delta_{j}^i$, где $i,j=1,2,3$.
Коммутаторы $[X_i,X_j]=c_{ij}^k{X_k}$. В силу условий на собственные значения $ad_{X_1}$ структурные константы $c_{12}^1,c_{13}^1$ не равны одновременно нулю.
Отличными от нуля могут быть также $c_{23}^1,c_{23}^2,c_{23}^3$. Другие структурные константы обязательно нули.
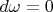
1-форма $\omega=c_{23}^3{\omega^2}-c_{23}^2{\omega^3}$ замкнута,т.е. $d\omega=0$ (проверяется прямым вычислением). Сл-но, она точна из-за односвязности $\mathbb{R}^3$ и существует гладкая функция $\psi$, определенная всюду на $\mathbb{R}^3$ такая, что $d\psi=\omega$.
$d({e^\psi\omega^2})={e^\psi}(d\psi\wedge\omega^2+d\omega^2)={e^\psi}(-c_{23}^2{\omega^3}\wedge\omega^2+c_{23}^2{\omega^3\wedge\omega^2})=0$.
Т.о. $e^\psi\omega^2=dV$, где $V$ - гладкая функция всюду определенная на $\mathbb{R}^3$ и не имеющая экстремумов. $X_2{V}=e^\psi>0$. Ясно, что вдоль любой траектории $X_2$ функция $V$ возрастает и периодических траекторий
у $X_2$ быть не может. А поскольку $X_2$ выбиралась произвольно, то утверждение доказано для любого поля неколлинеарного $X_1=X$.
Теперь, что касается поля $X_1$. Похожими рассуждениями желающие могут доказать утверждение об отсутствии периодических траекторий и для него.