Пусть

— произвольное векторное пространство.
Как известно, всякое линейно независимое подмножество

можно увеличить до базиса пространства

,
и этот факт легко доказывается с помощью леммы Цорна.
Справедливо ли следующее «двойственное» утверждение
и безошибочно ли его «двойственное» доказательство?
Теорема. Всякое порождающее* подмножество 
можно уменьшить до базиса пространства  .Доказательство
.Доказательство. Пусть
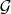
— упорядоченное по включению
множество всех порождающих подмножеств

.
Поскольку всякая цепь

имеет нижнюю границу

,
согласно лемме Цорна любой элемент

можно уменьшить до минимального

.
Такое множество

является базисом пространства

,
поскольку оно порождающее (так как принадлежит
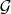
)
и линейно независимое (так как минимально).

__________
* Подмножество

называется
порождающим,
если линейная оболочка множества

равна

.
P.S. Хотел сначала разместить в головоломках, но передумал:
студентам это может быть полезно, а остальным — забавно.



