Я полагал, что так должно быть всегда, и знак минус это непременный атрибут пространственных компонентов 4-ковектора.
Это рассуждения на уровне "знак минус - это непременный атрибут глубины". Ну с чего бы? Пусть в одном месте обозначено

- высота, и глубина 5 метров обозначается

А в другом месте взяли другое обозначение:

- глубина, и ту же самую глубину 5 метров обозначили

И где тут знак минус? Ищите его днём с огнём - не найдёте.
Пусть мы имеем какую-то скалярную функцию
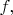
и от неё 4-градиент

Что означает знак минус в выражении

? Он означает, что если мы захотим воспринимать 3-мерную часть

как векторное поле, мы должны взять его с минусом, то есть, соответственно,

Но для чего это? Для того, что если мы поднимем индекс, то получим соответствующий вектор

и нам надо не забыть развернуть пространственную часть (отсюда формула в сноске, которую вы упоминаете). А нам это вообще надо - поднимать индекс? Может в жизни никогда не понадобиться. Ну и забудьте тогда про это. Просто помните, что 4-градиент

складывается из производной по времени, и 3-градиента.
Я, если честно, вообще не помню формулу

Потому что я её никогда не использую. Мне не надо возвращаться к 3-мерным векторам для 4-векторов, что контравариантных, что ковариантных. Я всего лишь помню два правила: векторы с разными индексами умножаются "компонента на компоненту", а векторы с одинаковыми индексами - с учётом сигнатуры метрики, то есть три последних слагаемых с минусом.


Есть и ещё более простой способ взгляда на ситуацию: вообще писать все индексы снизу, а при умножении (свёртке) использовать сигнатуру метрики. Например, такой способ очень любил Фейнман, и он себя оправдывает в большей части расчётов (СТО, КЭД и КТП, например - трудней только в ОТО) (формально этот способ соответствует тому, чтобы перейти в евклидово пространство с формально умноженными на

пространственными координатами). Можете его использовать в выкладках "для себя", только если преподаватель на зачёт требует всё правильно, то для него пишите аккуратно.
-- 16.10.2014 22:26:12 --Замечание в сторону. Как проверить и убедиться, что

а не, скажем, наоборот,

? Ответ: применить к ним преобразования Лоренца. Если компоненты будут переходить друг в друга правильно, то мы угадали знак.