Вот, что несколько часов назад написал Тао.
In my experience with these sorts of abstract attempts to solve the Navier-Stokes regularity problem, the difficulty is often concealed in some inconspicuous interchange of limits (or interchange of limit and integral, etc.), and usually at a part of the paper where the author is not being as careful and detailed as he or she is in other parts of the paper.
That said, the limit that concerns me the most from what I have read (I could get as far as Section 5 without any knowledge of Russian, but the crucial Section 6 has defeated me) is the limit
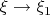
, and in particular the claim that the identity (i) on page 26 continues to hold in the limit
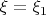
, which is crucially used in the first multiline display on that page. It is important here that one has strong convergence in the limit
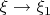
; weak convergence would only give an upper bound for the norm of
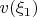
, rather than an exact identity, which would not be useful for the argument given here. Unfortunately the proof of this convergence is buried somewhere in Section 6, which I was not able to penetrate, but this may be something worth focusing on. (It was also a bit ambiguous from the text whether

really is permitted to be infinite here; this could be a related issue.)
From what I can gather from Section 5, the strategy of proof is to take the Navier-Stokes solution
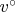
and deform it by an additional flow (in the
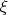
variable) in such a way that the limit (at
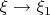
) becomes an eigenfunction of the Laplacian at each fixed time, at which point the contribution of the nonlinearity can be handled. The problem with these sorts of arguments is that the mass or energy could bubble off to infinitely high frequencies, and so the eigenfunction that appears in the (weak) limit is not actually capturing all of the mass or energy of the original solution. (This is similar to how weak solutions to Navier-Stokes equations are not known to obey the energy identity; instead, one can only prove a one-sided energy inequality, which is significantly less useful.)