Есть такой вопрос касательно теории множеств. Если множество, скажем
А, является элементом другого множества (не включено, а именно является элементом), скажем
В, можно ли дублировать элементы множества
А в множестве
В и тем самым говорить что возможна ситуация, в которой есть элемент, принадлежащий множеству
А и одновременно являющийся отдельным элементом множества
В?
чтобы выглядело примерно так:


То есть возможна ли ситуация

и

и
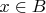
?
Опять таки - вопрос не в том, чтобы такое соблюдалось постоянно, а в том, возможно ли в отдельных случаях? Просто я еще не до конца эту тему понимаю, но желаю разобраться.
Навеяно первой же тридцаткой упражнений в учебнике "Тишин В.В. Дискретная математика в примерах и задачах"
Надеюсь, понятно спросил.