Попытаюсь довести почти детективную историю до логического конца.
Существуют расхождения между ожидаемым (психологически) результатом и теорией вероятности. Возьмем самый простейший пример, бросание абсолютно правильной монеты. При каждом броске монеты вероятность выпадения орла (

) и решки (

) одинаковые и равны 0.5. Даже при выпадении подряд ста «орлов» вероятность выпадения решки по классической теории вероятности не увеличивается. Ясно, что у монеты нет памяти, и она не знает, что выпало раньше , поэтому вроде бы очевидно, что вероятность при любых сериях выпадения остается равной 0.5, но в то же время, хорошо известно, что выигрывает тот игрок, который запоминает число выпадений орла и решки, предполагая , что частота их появления должна быть одинаковой и равномерной.
С вопросом как выйти из парадокса обратился вначале к математикам форума (
topic48349.html), затем к экономистам(
topic49410.html) , но те отфутболили опять к математикам. В итоге, попытался решить проблему сам.
Конечно, можно использовать все каноны математики, а именно: построить доверительный интервал и проверить статистическую гипотезу. Но стоит ли усложнять решение задачи, если такое решение наглядности не прибавит , тем более что в данном случае не проверяется правильность монеты.
Бросание монеты есть конкретный физический процесс, и потому мы можем избавиться от "дурной" математической бесконечности. Введя параметр N , получил соответствующую формулу -
topic49410.html . Оказалось, что, если параметр N ( по сути выборка) определять исходя из предположения, что при 0.5N бросаниях решка (

) выпадет хоть один раз, то формула сильно упрощается и нет необходимости определять сам параметр . (Так , например, опыт показывает, что при десятикратном бросании монеты, решка или орел выпадут по крайней мере один раз). Исходя из этого принципа получим на первый взгляд (!) убийственно простую и очевидную ( после того как ее получили) формулу:

(1)
И тут оказалось, что график этой функции
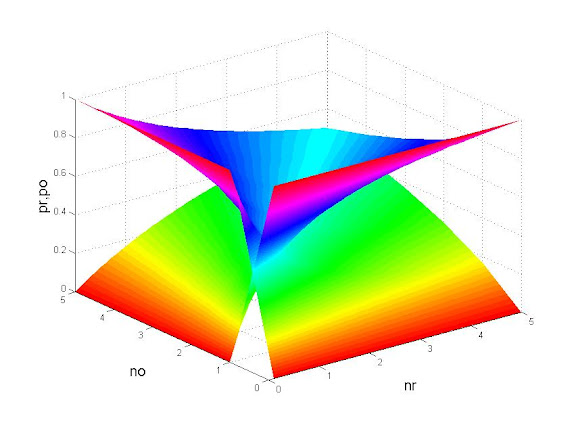
при небольшом числе бросаний монеты – до десяти - почти совпадает с графиком регуляризованной неполной бета-функции ( параметры функции приняты нестандартные):

(2)

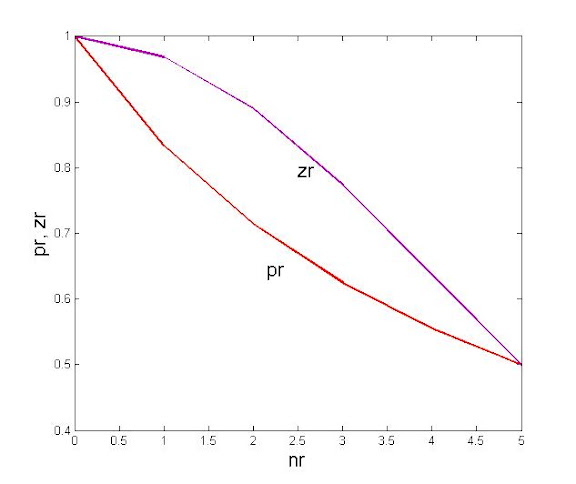
Как видим, вероятность появления решки определяется через частоту появления орла. И наоборот, вероятность появления орла определяется через частоту появления решки. Природа пытается соблюдать полную симметрию. Иначе говоря , формула (1), и бета-функция показывают «амплитуду колебания» вероятности в ту и другую сторону как колеблющаяся струна. Но если, по формуле (1) симметрия достигается плавно и струна способна отклониться как угодно далеко от нейтрального положения, то бета-функция нам показывает, что такое свободное беспредельное отклонение невозможно. Это особенно хорошо видно при выборке(бросании монеты) более 10.
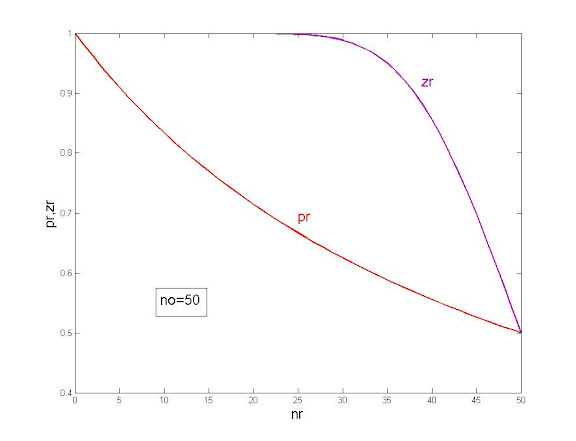
Напрашивается аналогия с натянутым луком. Нельзя натягивать тетиву лука как угодно сильно, есть предел натяжения, при котором тетиву следует отпустить, так как ее дальнейшее натяжение не увеличит дальность полета стрелы, а грозит лишь одним, поломкой лука. Косвенно это видно из графика бета – функции. Поэтому априори, на мой взгляд, бета-функция ( в том виде как она приведена в формуле (2)) дает результаты с бросанием монеты точнее, чем формула (1).