nn910 писал(а):
Тут 19 точек -7 с именами и 12 анонимных по сторонам и вершинам некого шестиугольника
Блин, точно, я эти точки пропустил

, жаль, поторопился. Придется другую конфигурацию искать. Или эту как-то подправлять. (ну хоть для 19 точек можно считать решенным

)
TOTAL писал(а):
Как отождествлять одни пять точек с другими пятью точками?
Видимо, произвольно. Если К - искомая конфигурация точек и прямых и в ней есть 5 точек общего положения, то можно их отождествить с данными, а остальные элементы достроить. Можно считать, что, например,

даны, а остальные точки надо достроить. Тогда

, точку

выбираем на
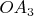
, а остальные точки достраиваем. Главное - конфигурацию найти, а построить несложно.