maxal писал(а):
Ограничение сверху на

- это сумма знаменателей чисел

и

. Дело в том, что если

, где
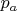
,

,

и

- натуральные числа, то

При этом эта верхняя грань достижима на соседних членах
рядов Фарея, причем в этом случае

представляет собой несократимую дробь.
Отсюда следует и алгоритм для нахождения искомого числа с наименьшим знаменателем:
1) если

и

являются соседними элементами ряда Фарея

, то решение уже указано выше;
2) в противном случае нужно "достроить" все дроби ряда Фарея

, находящиеся между

и

, и выбрать из них дробь с наименьшим знаменателем. Для этого можно начать с чуть большего отрезка (покрывающего
![$[a,b]$ $[a,b]$](https://dxdy-04.korotkov.co.uk/f/f/e/4/fe477a2781d275b4481790690fccd15f82.png)
) ряда

и достроить его стандартным образом (см. ссылку выше) до отрезка ряда

Сложность здесь пропорциональна разности знаменателей

и количеству дробей в

, находящихся между

и

.