мат-ламерВы спрашивали про
квантовую запутанность, так что классический язык не годится. Начинайте сразу с квантового; простой и довольно общий пример таков:
Пусть некий квантовый объект допустимо считать "состоящим из двух частей", 1 и 2. Например, источник раз за разом одинаково испускает "пару частиц, летящих в противоположные стороны". Пара частиц, скажем два электрона, здесь играет роль квантового объекта. "Раз за разом" нужно, чтобы иметь статистический ансамбль таких пар - чтобы у нас была возможность накопить статистику тех или иных измерений над частицами.
Обозначим символом

базисные векторы состояний части 1. Здесь

пробегает множество числовых значений; это спектр значений какой-то конкретной физической величины.
Напомню, что согласно принципу суперпозиции в КМ произвольное чистое состояние части 1 (т.е. когда объект 1 рассматривается как самостоятельный, ни с чем не запутанный объект, как замкнутая система) запишется в виде линейной комбинации базисных состояний:

Квадрат модуля каждого коэффициента,

дает вероятность обнаружить у объекта 1 данное значение

измеряемой физ. величины. Измерениям разных физ. величин будет соответствовать разложение одного и того же вектора состояния

по разным базисам.
Аналогично пусть

- базисные векторы состояний части 2. Тогда:

есть базисные векторы состояний объекта, состоящего из частей 1 и 2. И тогда лин. комбинация

описывает произвольное состояние объекта, где коэффициентами определяется вероятность

обнаружить (при измерении физ. величин) у части 1 значение

и у части 2 значение
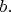
Обратите внимание: в общем случае

не разбивается на сомножители, зависящие в отдельности от

и
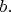
В этом случае, т.е. когда

части 1 и 2 здесь считаются "перепутанными". Объясняется этот термин следующими простыми соображениями.
Пусть через приличный промежуток времени после приготовленя объекта мы совершили акт измерения физ. величины у части 2, и получили результат

(Например, измерили прибором Штерна - Герлаха проецию спина на ось

у электрона 2, в то время как электрон 1 уже, как говорится, "улетел хрен знает куда" от этого прибора. Если Вы умеете описывать состояния поляризации фотонов, то лучше рассмотрите пару фотонов - такой пример будет ближе к реальным экспериментам, хотя пример с проекциями спинов электронов, имхо, чуть проще).
Если над частью 1 измерение ещё не производилось, то её все ещё следует описывать по прежним правилам КМ. Но теперь вектор состояния системы не должен включать суммирования по всем

ибо мы уже знаем что измерение над частью 2 дало конкретное значение:

Значит, надо записать "усечённый" (редуцированный) вектор состояния системы:

.
Как видим, он уже имеет форму произведения индивидуальных векторов состояния частей 1 и 2:

,
где вектор состояния части 2 есть

- он описывает лишь уже известный нам результат измерения (

), а вот вектор состояния части 1 все ещё имеет вид суперпозиции (лин. комбинации):

.
Что же здесь примечательного? А то, что он зависит от

! Это во-первых. А во-вторых, это выражение зависит и от выбора физической величины для измерения над частью 2: ведь от выбора измеряемой величины для 2 зависит конкретный базис

и распределение вероятности для неё, а следовательно, и численные значения коэффициентов

Совершенно аналогично можно рассмотреть измерение над 1 (с каким-то результатом

) без измерений над 2. Тогда, сразу же после измерения над 1 состояние части 2 будет:

.
Как видим, оно зависит от того, что измерялось у части 1 (т.к. числа

зависят от выбора базиса

), и от того, какой обнаружился результат

.
Вот такие зависимости состояний одной частицы от измерений над другой частицей в данном примере и называют "квантовой запутанностью" частиц 1 и 2, или - "нелокальным влиянием" одной частицы на другую, причём - мгновенным влиянием, или "парадоксом Эйнштейна - Подольского - Розена".
Замечу, что "парадокс" (в смысле - противоречие с классическим представлением о распространении взаимодействий между объектами и их локальности) возникает в рассуждениях о векторе состояний, как о динамической характеристике, присущей каждому
экземпляру частиц. Это сродни "парадоксу редукции волновой функции". У тех же людей, кто предпочёл статистическую интерпретацию КМ (вроде Фейнмана; ну, и меня тоже :)), таких "парадоксов" нет: мы рассматриваем векторы состояний как способ
статистического описания квантового ансамбля систем. До акта измерения теория даёт распределение вероятности

лишь как функцию двух аргументов -

и
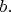
После акта измерения над одной из частиц, когда становится известным конкретное значение одного из аргументов, достаточно рассматривать часть этого распределения вероятностей -

при фиксированном значении одного из аргументов как функцию оставшегося аргумента. Понятно, что отбросить ставшую ненужной часть распределения можно мгновенно - сразу же вслед за измерением.
Понятно также, что статистическая интерпретация векторов состояний не отменяет (и не обесценивает!) отличительной специфики квантовых распределений вероятности. Ведь КМ выдает такие распределения

, которые во многих задачах сильно отличаются от классических ожиданий из каких-нибудь "теорий скрытых параметров". Вычисленные по уравнениям КМ функции

уже включают все возможные "квантовые корреляции", ведут к нарушениям неравенств Белла (и такие нарушения подтверждены экспериментально). С этой точки зрения "квантовая запутанность" в КМ-задачах - избыточный термин; в мат. аппарате КМ всё необходимое есть и без этих "парадоксальных" слов.