А оно вообще неправильное - по нему

Большое спасибо. Предполагалось изначально, что четвёрка не содержит одинаковых компонент. Вопрос к аудитории: могут ли компоненты быть равными, если четвёрка - линейное пространство?? Но в самом общем случае мы имеем примерно следующее:
1. Определяем упорядоченную пару

2. Пишем рекуррентное определение

-ки

если


если

3. Теперь пишем теорему, что

равны только тогда, когда

для всех

,

.
База индукции. Есть такой факт

тогда и только тогда, когда

и

. Интересно, что в литературе его считают иногда аксиомой, а иногда теоремой.
Предположение.  Следствие.
Следствие. Теперь заметим, что

само по себе является парой, так же как и

, откуда

(см.
База индукции)
Теперь можно я возьму не ваш пример, а две тройки

и
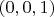
? Их нельзя считать равными, так как


Что одновременно означает финиш — получается, Kras даже с множествами не разобрался!
arseniiv, а вы в состоянии, пользуясь, скажем, рекуррентным определением, выписать случай

? И насколько это целесообразно и необходимо, если цель - понять что такое линейное пространство?
А ещё лучше (по краней мере в данном случае) определить упорядченную

-ку аксиоматически, тем самым явно подчеркнув нетривиальный факт независимости определения и основных свойств линейного пространства от конкретной теоретико-множественной (или иной) реализации это самой

-ки.
, расскажите подробнее, если не трудно.