При исследовании свойств системы сжатых капель потребовалось доказать следующее утверждение:
На плоскости имеется точка

, через которую проведена ось

. На некотором участке плоскости, размеры которого малы по сравнению с расстоянием до точки

, действует преобразование

, переводящее отрезок

, перпендикулярный оси

и пересекающий ее в точке

, в дугу окружности

радиусом

с центром в точке

с сохранением расстояний вдоль дуги.
Утверждается, что если на месте отрезка

будет расположена дуга

радиусом

, пересекающая ось

в той же точке

с центром

, лежащем на оси

, то данное преобразование

переведет ее в дугу, так же расположенную, но с иным радиусом

таким, что:

Доказательство:
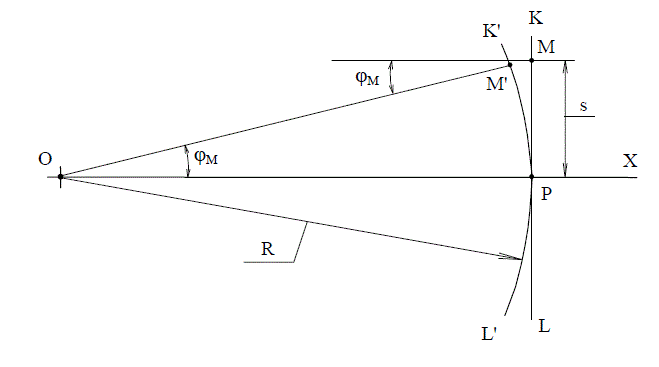
Выберем на отрезке

произвольную точку

, отстоящую от

на расстоянии

(первый рисунок). Когда рассматриваемое преобразование переведет отрезок

в дугу

, точка

займет новое положение

такое, что расстояние

, измеренное вдоль дуги, не изменится, и останется равным

, согласно условию. При этом нормаль к исходному отрезку

, проведенная через точку

, повернется на угол

и займет положение отрезка

.
Теперь рассмотрим преобразование дуги

с радиусом

, у которой центр кривизны

лежит на оси

слева от точки

.
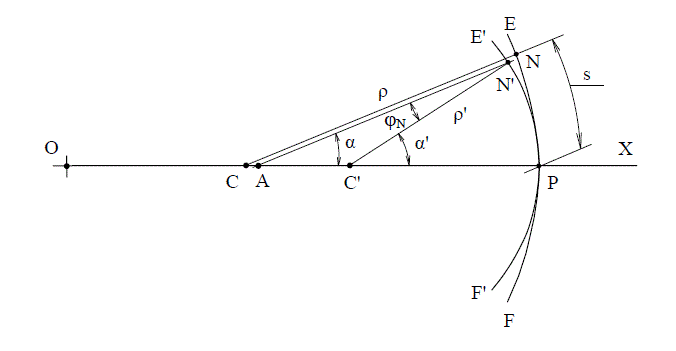
На этой дуге отметим точку

, расположенную на том же расстоянии

от точки

, измеренном вдоль дуги. Очевидно, что эта точка не совпадает с точкой

на отрезке

, но они могут быть сколь угодно близкими, если выбрать расстояние

достаточно малым. Ввиду этого можно считать, что в результате преобразования

дуга

изогнется так, что нормаль, проведенная к ней в точке

, повернется в ту же сторону и на тот же угол

, что и у отрезка

в точке

. При этом нормаль займет положение

(второй рисунок). Проведем через точку

прямую, параллельную

до пересечения с осью

в точке

и рассмотрим треугольник

. Как известно, внешний угол
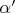
равен сумме внутренних, не смежных с ним:

но

и

. Тогда с учетом ранее приведенного выражения для

получим:

что после сокращения на

даст

что и требовалось.
Можно ли принять такое доказательство?