что
собственная длина окружности больше

нет, в этой системе отсчета периметр эллипса на котором мгновенно располагаются все кончики спиц МЕНЬШЕ чем

. но кончики спиц двигаются по нему неравномерно, с переменной угловой скоростью, внизу с большим шагом вверху с малым, поэтому если самый большой шаг между ними умножить на их количество, то получается

, но это произведение не является длиной периметра.
Я же писал не о периметре колеса в системе отсчета неподвижного отрезка, а о
собственной длине окружности. Конечно периметр колеса в какой либо СО другой, но он не может превышать
собственную длину его окружности. При движении колеса по неподвижному отрезку, прикладываемый к нему сегмент

окружности - неподвижен, поэтому обязан иметь собственную длину. В вашем (совершенно правильном согласно СТО) расчете получается, что сумма всех

собственных значений длины сегментов окружности больше

.
Представленный вами расчет соответствует случаю, когда курвиметр представляет собой не набор спиц,
как так? я именно для кончиков спиц сделал рассчет, для их конечного количества. для диска пришлось бы переходить к бесконечному их количеству и пределам и всяким деформациям и напряжениям, но вы облегчили мне задачу, сделав ее более наглядной без лишних сущностей
Совершенно верно, я намеренно убрал обод колеса из рассмотрения, чтобы облегчить рассмотрение, и не только вам, но и всем

. Но ваше решение (результат, а не расчет) не соответствует самой же СТО, т.к. отрезок

получается больше своей собственной длины.
Если же колесо представляет собой набор спиц, то причин увеличивать длину (относительно своей собственной длины) у сегмента, соприкасающегося с измеряемым отрезком, - нет.
вот поэтому и не надо решать задачи в сто путем "наложения эффектов" и не размышлять есть тут причины наложить эффект или нет причин. считайте в лоб, преобразуйте уравнения движения интересующих вас точек из исо в исо, а "эффекты наложатся" автоматически. преобразуйте уравнения движения двух не связанных друг с другом мух и тогда выясните "есть причины" к изменению расстояния между ними в новой исо или их нет
Задачи решать можно по-разному, но вот физический смысл в физических задачах необходим.
Можете назвать физическую причину удлинения отрезка, когда на него не действуют никакие силы?
движение материальных точек, берущихся в качестве его краев, с разной скоростью. вполне физическая причина. скорость одинакова - разность координат

не меняется, иначе меняется. преобразовав скорости двух независимых точек в другую исо вы обнаруживаете что они разные
Точки

и

не независимы, они жестко связаны с центром колеса.
-- 26.12.2014, 08:01 --Здесь вот что происходит. Относительность одновременности гласит, что когда в нижней ИСО точки А и В соприкоснулись с отрезком одновременно в верхней ИСО сперва отрезка касается точка А, и позже через некоторое время точка В,
Точки

и

касаются отрезка не одновременно в обоих ИСО . Но в обоих ИСО в момент касания второй точки и отрезка - первая точка уже соприкасается с отрезком, удовлетворяя тем самым требование одновременного прикладывания концов линейки к измеряемому отрезку.
-- 26.12.2014, 08:46 --Я думаю, что система со спицами - эквивалентна диску, потому, что расстояние между спицами жестко определено их связью на оси- это не независимое движение двух тел.
Насчет жесткости связи в центре колеса вы совершенно правы, и конечно, концы спиц не являются независимыми. Но система спиц НЕ эквивалентна диску. На вращающемся диске происходит растяжение (упругая деформация) в каждой его точке, кроме центра вращения. Соответственно на ободе диска все его участки растянуты в

раз. Поэтому, если мы рассуждаем физически, когда диск катится по измеряемому отрезку и его участок, соприкасающийся с отрезком, неподвижен, то он отмеряет на отрезке в

раз больший интервал, т.к. растянут (его растягивают претерпевающие Лоренцево сокращение другие участки обода). Если же колесо представляет собой набор спиц, то причин для растяжения неподвижного сегмента нет.
Здесь можно возразить, что центр колеса не математическая точка и должен иметь хоть и малый, но размер, поэтому Лоренцево сокращение его частей может влиять на величину отрезка

. Это легко учесть. Пусть центр колеса является сколь угодно малым, но сплошным диском. Т.к. этот диск имеет сколь угодно малый размер, то линейная скорость точек его обода сколь угодно мала по сравнению со скоростью поступательного движения этого диска как целого. Это означает, что релятивистских эффектов, связанных с вращением этого маленького диска нет, т.е. преобладают релятивистские эффекты, связанные с его движением как целого. При движении же этого диска как целого все его продольные размеры сокращаются, значит сокращается и бесконечно малый участок его обода, связывающий две соседние спицы, которые в данный момент соприкасаются с измеряемым отрезком. Таким образом, Лоренцево сокращение центра курвиметра может привести только к уменьшению отрезка

, соприкасающегося с измеряемым отрезком. Но этот эффект только усугубляет противоречие, т.к. длина отрезка в ИСО, где он неподвижен, становится не равной, а большей, чем

, в то время как в ИСО неподвижного центра курвиметра длина отрезка
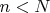
.