Найти коэффициент при x в разложении

[Nurzery[Rhymes]]

Великая по "глубине" задача, в которой я не могу разобраться. Условие: допустим, вариант задачи звучит как "найти коэффициент при $x^{30}$ в разложении $(3-x^2$+ x^5)^{19} ".
Это задача на полиномиальную формулу. Для возведения полинома в небольшие степени мы делали так:
Например, раскладываем $(a+b+c)^5$. Строим все возможные уникальные разложения числа $5$ на сумму трех чисел, к примеру, $2+2+1$. Коэффициент при соответствующем слагаемом будет равен $P(2,2,1)$.

А как применить эту формулу к решению моей задачи? Для больших степеней выписывать разложение не оптимально, да и число $19$ можно разложить на сумму трех чисел большим количеством способов. Нужен какой-то аналитический подход. Какой?

[ИСН]

Nurzery[Rhymes] в сообщении #938807 писал(а):

Для больших степеней выписывать разложение не оптимально

Оно, может, и не оптимально, но всё остальное ещё хуже.

[Sonic86]

Да как бы не факт, что есть какая-то более простая для вычисления формула, чем та, которая получается из полинома Ньютона.
Почему бы и не выписать сумму для коэффициента явно (всего-то 2 действия), потом просто посчитать ее. (я вот за 2 минуты выписал, там кстати всего 4 слагаемых)

Nurzery[Rhymes] в сообщении #938807 писал(а):

Коэффициент при соответствующем слагаемом будет равен $P(2,2,1)$.

Это уже некие утонченности, которые можно юзать, если Вас заставляют коэффициенты считать ручками. Если явного ответа не требуется, то это только усложняет формулу для коэффициента.

[Nurzery[Rhymes]]

Sonic86 в сообщении #938810 писал(а):

Почему бы и не выписать сумму для коэффициента явно (всего-то 2 действия), потом просто посчитать ее..

Я не понимаю, как вычислять значение коэффициента при данном слагаемом. Объясните общий принцип?
И еще, такого слагаемого, как в условии, в разложении просто нет. Штука $x^{30}$ может быть в составе какого-то слагаемого, но никак не сама по себе. Некорректность условия, но нам дают задачи именно в таком виде.

[nnosipov]

Nurzery[Rhymes] в сообщении #938814 писал(а):

И еще, такого слагаемого, как в условии, в разложении просто нет. Штука $x^{30}$ может быть в составе какого-то слагаемого, но никак не сама по себе. Некорректность условия, но нам дают задачи именно в таком виде.

Вот эта задача:

Nurzery[Rhymes] в сообщении #938807 писал(а):

"найти коэффициент при $x^{30}$ в разложении $(3-x^2+ x^5)^{19}$".

вполне корректна. Потрудитесь понять условие.

[Nurzery[Rhymes]]

nnosipov в сообщении #938820 писал(а):

Nurzery[Rhymes] в сообщении #938814 писал(а):

И еще, такого слагаемого, как в условии, в разложении просто нет. Штука $x^{30}$ может быть в составе какого-то слагаемого, но никак не сама по себе. Некорректность условия, но нам дают задачи именно в таком виде.

Вот эта задача:

Nurzery[Rhymes] в сообщении #938807 писал(а):

"найти коэффициент при $x^{30}$ в разложении $(3-x^2+ x^5)^{19}$".

вполне корректна. Потрудитесь понять условие.

Уже понял. Получится многочлен от одной переменной $x$, а не от нескольких, поэтому степени при $x$ складываются и могут дать значение $30$. А как ее решать? И есть ли сборники с такими примерами и ответами, чтобы можно было потренироваться?

[nnosipov]

Nurzery[Rhymes] в сообщении #938823 писал(а):

А как ее решать? И есть ли сборники с такими примерами и ответами, чтобы можно было потренироваться?

Ответ можно проверить в любой системе компьютерной алгебры. Решать в лоб, используя полиномиальную формулу.

[Nurzery[Rhymes]]

nnosipov в сообщении #938826 писал(а):

Nurzery[Rhymes] в сообщении #938823 писал(а):

А как ее решать? И есть ли сборники с такими примерами и ответами, чтобы можно было потренироваться?

Ответ можно проверить в любой системе компьютерной алгебры. Решать в лоб, используя полиномиальную формулу.

Я нашел аналитическое решение, а не в лоб: http://wiki.seekland.info/%D0%9F%D0%BE% ... 0%BC%D0%B0
Хочу потренироваться искать ответ через систему уравнений. В мейпле функция expand не выводит результат возведения скобки в степень в виде многочлена, а упрощает его вид. Там получается сумма скобок в некоторых степенях.
А, нет, эта функция все-таки разворачивает выражение в многочлен. С некоторыми другими выражениями она не справлялась.

[nnosipov]

Nurzery[Rhymes] в сообщении #938827 писал(а):

Я нашел аналитическое решение, а не в лоб:

Это и есть в лоб.

[Sonic86]

(Оффтоп)

Nurzery[Rhymes] в сообщении #938827 писал(а):

Я нашел аналитическое решение, а не в лоб: http://wiki.seekland.info/%D0%9F%D0%BE% ... 0%BC%D0%B0

Так неинтересно. Задача в 3 действия. 1-е действие Вам сообщили - применение полинома Ньютона. Зачем же было гуглить.
Мапле здесь не нужен, выключите его.

[Nurzery[Rhymes]]

Sonic86 в сообщении #938833 писал(а):

Так неинтересно.

Комбинаторика вообще невыносимо скучна. Хочется быстрее все сдать и забыть ее. В выборе одной из комбинаторных формул для решения задач вообще нет никакой логики: часто объекты считаются одинаковыми, когда это даже физически невозможно, ибо они разные на уровне состояния молекул и атомов, из которых они состоят. Условие комбинаторных задач можно перевернуть как угодно. Ни в одной другой области математики такое не возможно.

-- 01.12.2014, 21:46 --

Придумал себе задачу вычислить коэффициент при $x^{24}$ в разложении $(1 - 3x^2 + 5x^4)^8$. По алгоритму из той статьи получил систему:

$ \left\{ \begin{array}{rcl} &x+y+z=8& \\ &2y + 4z = 24& \\ \end{array} \right. $

Как из нее найти показатели степеней $x,y,z$?
Мы ищем решение в целых числах, кроме того, показатели степеней не должны быть отрицательными. Я выразил две переменные через одну, перед этим подставив выражение $y$ из второго уравнения в первое:

$ \left\{ \begin{array}{rcl} &x=3z-4& \\ &y=12-2z& \\ \end{array} \right. $

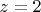
Пусть $z=2$, т.к. при меньшем значении получим отрицательное число.
$ \left\{ \begin{array}{rcl} &x=6-4=2& \\ &y=12-4=8& \\ \end{array} \right. $

Пусть $z=3$

$ \left\{ \begin{array}{rcl} &x=9-4=5& \\ &y=12-6=6& \\ \end{array} \right. $

Подставляем различные целые $z$ до тех пор, пока не начнут появлятсья отрицательные значения. Получим упорядоченные тройки $(x,y,z)$:

$(2,8,2), (5,6,3), (8,4,4), (11,2,5), (14,0,6)$
Ни одно из этих решений не удовлетворяет системе :(
Ура, я решил! Была арифметическая ошибка.

[ИСН]

Начиная с $x=3z-4$, всё куда-то покатилось.

[Sonic86]

Nurzery[Rhymes] в сообщении #938836 писал(а):

Ура, я решил! Была арифметическая ошибка.

Ответ-то будет?

(болтовня)

Nurzery[Rhymes] в сообщении #938836 писал(а):

Комбинаторика вообще невыносимо скучна.

Я не спец по комбинаторике, но я в этом сомневаюсь. В ней одно Рамануджановское $p(n)$ чего стоит. Производящие функции - хорошая и интересная штука. Мне также интересен принцип соответствия простых решений простым рассуждениям, в результате которых они получаются.

Nurzery[Rhymes] в сообщении #938836 писал(а):

В выборе одной из комбинаторных формул для решения задач вообще нет никакой логики: часто объекты считаются одинаковыми, когда это даже физически невозможно, ибо они разные на уровне состояния молекул и атомов, из которых они состоят.

Объекты в задачах - это в точности то, что о них говорится. От всего остального следует абстрагироваться. Т.е. если в задаче не говорится (и не подразумевается), что объекты из чего-то состоят, то от этого факта следует абстрагироваться.
Насчет отсутствия логики - Вы неправы: логика есть, вы описание условия должны транслировать в комбинаторную формулу, элементы текста перевести в элементы формулы. Если Вы чего-то не видите - это Ваша ошибка, а не комбинаторики.

Nurzery[Rhymes] в сообщении #938836 писал(а):

Условие комбинаторных задач можно перевернуть как угодно. Ни в одной другой области математики такое не возможно.

Это какие-то бессмысленные фразы. Что такое "перевернуть"?

[iifat]

Nurzery[Rhymes] в сообщении #938836 писал(а):

часто объекты считаются одинаковыми, когда это даже физически невозможно, ибо они разные на уровне состояния молекул и атомов, из которых они состоят

Боюсь представить себе, как вы просите взвесить килограмм яблок с такими принципами.

[Sonic86]

(Оффтоп)

iifat в сообщении #939087 писал(а):

Nurzery[Rhymes] в сообщении #938836 писал(а):

часто объекты считаются одинаковыми, когда это даже физически невозможно, ибо они разные на уровне состояния молекул и атомов, из которых они состоят

Боюсь представить себе, как вы просите взвесить килограмм яблок с такими принципами.

А что не так с килограммом яблок? Кладем на весы и вуаля, каждая молекула имеет свой вес, все суммируется. Или Вы имеете ввиду вопросы типа "Одно яблоко весит 250 грамм, сколько весит 2 яблока?"