Условие:В окружности

проведены две пересекающиеся перпендикулярные хорды

и

. Доказать, что
 Решение:
Решение:Проведём диаметр

.
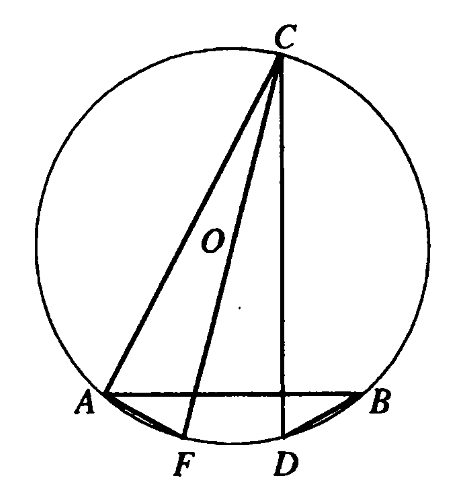
Докажем, что

как хорды, стягивающие равные дуги. Действительно,

(так как

),

(поскольку

- диаметр). Следовательно,

и

. В прямоугольном треугольнике

имеем

, откуда и

. Что и требовалось доказать.
Мне непонятен вот этот момент:

(так как

). Это откуда так получается?