Изначально есть прямой цилиндр радиуса

с прямой цилиндрической полостью радиуса

смещенной относительно центра цилиндра на

.
в области между вырезом и стенкой цилиндра надо решить

По оси

по условию задачи ничего не меняется. Тогда с помощью дробно линейного отображения делаю отображение кольца на кольцо







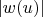


меня интересовало отображение кольца в центр цилиндра.
После дробно линейного преобразования, пересчитал коэффициенты Ламе и получилось

известно что

~

в старой области

, а в новой

(видимо в следствии этого перехода я сделал неверный вывод)
Поэтому вместо уравнения которое в 1 сообщении, вопрос немного меняется

, как решить:

Скорей всего я сделал ошибку еще раньше, но не вижу ее.
А еще может кто-нибудь пожалуйста порекомендовать литературу по решению задач, где решается уравнения Лапласа в области с вырезом ( на подобие этой)?