Я составил параметрическое уравнение плоскости
Не знаю, что такое параметрическое уравнение плоскости
Если говорить об уравнении в единственном числе, то векторно-параметрическое уравнение плоскости:

где

- параметры,
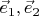
- направляющие векторы плоскости. Раскладывая это уравнение по координатам, получим параметрические уравнения плоскости (во множественном числе):

Хотя, как пишет Александров в своей книге, эту систему можно назвать
параметрическим уравнением - то есть в единственном числе, единственное число оправдано тем, что в действительности система трёх уравнений является лишь координатной записью одного уравнения.