Пусть

- множество множеств, обладающих этим свойством.
Тогда

.
Пусть

- множество минимальных по включению множеств из

.
Пусть

- минимальное по включению множество из

, не представляющееся как объединение множеств из

.
Поскольку

, то существует
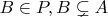
.
Если

или

, то либо оба эти множества принадлежат

(и

представляется как их объединение), либо нет, и

не минимально.
Для бесконечных неочевидно существование минимального множества, не представляющегося как объединение.