ошибки у Фихтенгольца

Munin · 30/01/06 72407

mishafromusa
Видимо, вы не о том, и не в курсе. Почитайте по ссылке.

mishafromusa · 12/02/14 808

Munin в сообщении #875288 писал(а):

mishafromusa
Видимо, вы не о том, и не в курсе. Почитайте по ссылке.

В каком месте не о том? Про Картана или про Лиувилля?

lena7 · 29/04/12 268

Лиувилль не дал алгоритма. Это сделал Риш в 1968.

mishafromusa · 12/02/14 808

lena7 в сообщении #875300 писал(а):

Лиувилль не дал алгоритма. Это сделал Риш в 1968.

Но Лиувилль сформулировал и доказал критерий интегрируемости в элементарных функциях,
Вербицкий ссылается на http://www-sop.inria.fr/cafe/Manuel.Bro ... ac98.ps.gz там на стр.15 теорема Лиувилля, я про это говорил.

-- 14.06.2014, 07:04 --

V_I_Sushkov в сообщении #874895 писал(а):

Коши не знал, что в рамках вещественных чисел это сделать невозможно, потому что у Лейбница дифференциалы в обозначениях производных и интегралов - бесконечно малые числа (именно числа), а у Лагранжа - нет. Его мы должны извинить.
Но вот многих из советских авторов извинить уже труднее, потому что они должны были знать о теории гипервещественных чисел (1960-е годы), в которой бесконечно малые числа Лейбница реализованы аккуратно.

Как метко заметил Арнольд в самом начале своей книжки "Геометрические Методы ОДУ," $dx$ -- это не какая-то мифическая бесконечно малая величина, а просто линейная функция касательного вектора. Поэтому всё понятно и без гипервещественных чисел. :-)

V_I_Sushkov · 12/06/14 61 Сант-Петербург, Россия

sergei1961 в сообщении #520412 писал(а):

Речь идёт только о трёхтомнике. <...> Долго думал, что ошибок в нём вообще нет (как и опечаток) и это эталон. Вот теперь знаю две. Добавляйте.

sergei1961, да, был культ личности.
Пополняю Вашу коллекцию. Я писал об этих ошибках
http://www.za-nauku.ru//index.php?option=com_content&task=view&id=1003&Itemid=31
http://www.spbstu.ru/publications/m_v/N_015/frame_15.html#top
Но здесь на форуме никто ничего не понял. Потому даю детальные разъяснения.
Фото страниц вставить я пока не научился.
Потому просто указываю страницы по изданию 1962 года, 1 том.

Все эти ошибки я отмечаю здесь не из-за буквоедства, а из-за того,
что видел и вижу их ужасное разрушающее воздействие на сознание
тысяч студентов и преподавателей.

Стр. 214. Здесь Г.М. утверждает, что формулу дифференциала из определения $y'(x) \Delta x$
якобы можно переписать в виде (5): $dy = y'(x) dx$ .
Это неверное утверждение, потому что (5) дает нам дифференциал только в двух случаях из трёх:
1) когда $x$ и $\Delta x$ - первичные переменные для комплекса всех переменных рассматриваемой задачи
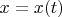
2) когда $x = x(t)$ (или ф-ция большего числа аргументов) и нам нужен дифференциал $dy$ из разложения $y(x(t+\Delta t))$ по степеням $\Delta t$
В третьем же случае, когда $x$ и $\Delta x$ - функция и ее приращение,
и нам нужен дифференциал из разложения $y(x+\Delta x)$ по степеням $\Delta x$
- надо пользоваться ф-лой дифф-ла из определения, ф-ла (5) становится неверна.
Если бы Г.М. сделал такую оговорку везде, дальнейших нелепостей не было бы.
Но из следующих страниц видно, что он делал эту оговорку все реже и реже и, наконец,
совсем перестал ее упоминать.
А все результаты без обоснования распространял на все три случая.

Стр. 215. Здесь Г.М. неосознанно приписывает Коши лишнее.
Да, Коши своей теорией пределов убрал с глаз долой бесконечно малые числа Лейбница
и в глазах современников перевел матанализ из мира бесплотных духов в мир реальных величин.
Но он не смог убрать б.м. числа из обозначений Лейбница.
Г.М. же верит, что и это удалось Коши.
И поэтому он осуществляет разрушительную для сознания студентов
тотальную подмену дифференциалов Лейбница
дифференциалами Лагранжа
в обозначениях Лейбница.

Стр. 216. Здесь есть оговорка Фихтенгольца, что рассуждения применимы
когда "икс - независимая переменная" но уже на следующей странице 217...

Стр. 217. ...здесь Г.М. уже забыл о своей оговорке с предыдущей страницы
и неверно утверждает, что формулу дифференциала всегда можно писать в виде (5)
Вот это свое неверное "всегда" он и называет "инвариантностью" дифференциала.
(у авторов до Г.М. я не видел термина "инвариантность", это явный плод пропаганды ТО).
На самом же деле эта "инвариантность", повторяю, наблюдается не всегда,
а только в двух случаях из трёх (см. стр. 214),
только в области использования формулы дифференциала суперпозиции двух функций.
Но не в полной области употребления дифференциала (того, что в определении)!
В третьем случае подстановка в $dy$ разложения $\Delta x$ по степеням $\Delta t$ даёт
сумму $dy = y'(x)\Delta x = \sum y'(x(t)) x^{(n)}(t) \frac {\Delta t^n} {n!}$
и желаемый Фихтенгольцу результат получить невозможно в принципе, даже если проделать еще
одну операцию выделения главной линейной части (в сумме справа).

Стр. 218.
Г.М. уверяет, что правило V (дифференцирования суперпозиции двух функций)
в обозначениях Лагранжа "всегда" выглядит так же, как в обозначениях Лейбница,
т.е. в виде правила сокращения дроби
Если бы Г.М. аккуратно следил за своей же необходимой оговоркой, он бы видел,
что это верно опять только в двух случаях из трёх (см. стр 214).
А вот в третьем случае правило V уже не выглядит как правило сокращения дроби:
$\frac {dy} {dx} = \frac {dy} {\Delta u} \frac {du} {\Delta x}$
(напоминаю: в левой части равенства дифференциалы Лейбница, в правой - Лагранжа,
приращения обозначены как всегда)

Стр. 241 Здесь Г.М. уже окончательно опускает свою оговорку и вот результат:
он уверяет, что в Лейбницевском обозначении старшей производной
дифференциалы Лейбница можно заменить дифференциалами Лагранжа и
разрешает читателям рассматривать результат такой замены как дробь.
Ну, если Фихтенгольц разрешил, то и воспользуемся его разрешением:
$\frac {d^{n} y} {dx^n} = \frac {d^{n}y} {du^{n}} (\frac {du} {dx})^{n}$
т.е. получили неверную общую формулу старшей производной суперпозиции двух функций.
Не говоря уже о том, что общую формулу вообще получить невозможно.
Это один из тех случаев рекуррентных вычислений, которые в принципе не сокращаются
до формулы n-ого члена последовательности.
Что же на самом деле должен был написать Фихтенгольц, заменяя дифференциалы Лейбница
дифференциалами Лагранжа ? Он должен был написать
$\frac {d^{n}y} {dx^n} = \frac {d^ny} {\Delta x^n}$
Здесь в левой части дифференциалы Лейбница, в правой части - Лагранжа.

-- 14.06.2014, 18:33 --

Стр. 242 Здесь Г.М. тоже не упоминает свою оговорку, но, действуя в её рамках,
он получает формулу второго дифференциала суперпозиции,
$d^2y = y''(x) dx^2 + y'(x) d^2x$ (3)
которая верна во всех трёх случаях.
Дело в том, что её можно получить из суперпозиции двух степенных разложений.
Т.е. здесь Г.М. получил верную всегда формулу, действуя методами, справедливыми лишь
в двух случаях из трёх. И не заметил этого.
Но ниже на этой же странице есть вопиющая ошибка Г.М. - "разобранный" им пример.
Он рассматривает две функции $y = x^2$ и $x = t^2$
Сначала он вычисляет второй дифференциал от суперпозиции $y = t^4$
(в отличие от него я использую правильные обозначения)
$d^2y=12t^2 \Delta t^2$
Это второй дифференциал из разложения $y(x(t + \Delta t))$ по степеням $\Delta t$ в точке $t$
Это эталонный результат, правильный.
Кроме того, он вычисляет тот же второй дифференциал по формуле (3) дифференциала суперпозиции
$d^2y = 2 dx^2 + 2x d^2x = 2 (2t\Delta t)^2 + 2t^2\Delta t^2 = 12t^2 \Delta t^2$
получил то ж самое,естественно.
И ещё он вычисляет нечто
$y''(x)dx^2$
Но что это такое?
Если это и в самом деле второй дифференциал, он должен был быть таким:
$d^2y = y''(x) \Delta x^2 = 2 ((t+\Delta t)^2 - t^2)^2 = 8t^2 \Delta t^2 + 8t \Delta t^3 + 2 \Delta t^4$
Т.е. это второй дифференциал из разложения $y(x + \Delta x)$ по степеням $\Delta x$ ,
выраженный через $t$ и $\Delta t$ - совсем другой дифференциал, который не имеет смысла сравнивать с только что полученным.
Но Фихтенгольц вычисляет именно произведение второй производной по икс на квадрат дифференциала функции икс (!)
- то есть вычисляет значение формулы, которая ЗАВЕДОМО НЕ ЯВЛЯЕТСЯ вторым дифференциалом
ни в том ни в другом разложении.
Заложив в вычисления неверную формулу он потом показывает, что результат не совпадает с предыдущими и отсюда делает какие-то выводы о какой-то "не инвариантности"...
Заложил в исходные условия ложь, как следствие получил очевидную ложь,
и на основании ложности следствия уверяет, что причиной его ложности является что-то другое, а не он сам!
Это что, математика или ловкость рук, извините?

Ну а следующие авторы массовых (и эталонных) советских учебников - Ильин и Позняк, Шилов, Кудрявцев и т.д. в этой теме следовали Фихтенгольцу и некоторые добавили ошибок еще более ужасных.
И совокупный тираж их по СССР - миллионы экземпляров книг!

-- 14.06.2014, 18:53 --

После этого описания скажу два слова на тему "что делать".
Надо не просто исправлять найденные ошибки, надо переписывать весь раздел заново,
заботясь о том, чтобы учащиеся овладевали сразу двумя языками:
и языком производных
и языком дифференциалов.
Только их совокупность обеспечит математическую грамотность обучаемых
и их способность выдвигать гипотезы и проверять себя.
Во времена Фихтенгольца под влиянием успехов Коши язык дифференциалов
был отодвинут на задний план, главной была производная.
От этой кособокости и пошли описанные мной выше проблемы.

lena7 · 29/04/12 268

V_I_Sushkov в сообщении #875399 писал(а):

Во времена Фихтенгольца под влиянием успехов Коши язык дифференциалов был отодвинут на задний план, главной была производная.

Я не знаю, что там у Фихтенгольца, но дифференциал и производная это одно и то же. И не надо мозги засорять лишними сущностями.

А Фихтенгольца уже не исправлять надо, а выкидывать. Устарёл он. Особенно учитывая, что значительная часть его посвящена тому, как жить в мире, где нет компьютеров.

Padawan · 13/12/05 4655

Oleg Zubelevich в сообщении #875275 писал(а):

у К-Ф отображение задается в бескоординатном виде. Элементу одного пространства поставлен в соответствие элемент другого пространства.

Padawan в сообщении #875249 писал(а):

Это определение ничуть не более инвариантно, чем $d^2f=\sum_{i,j=1}^n\frac{\partial^2 f}{\partial x^i\partial^x^j}dx^idx^j$ -- сохраняется только при линейных преобразованиях.

"более инвариантно"\"менее инвариантно" это демагогия. Речь шла о вполне конкретных вещах. А именно о том, в каком смысле у Фихтенгольца первый дифференциал инвариантен , и почему в этом смысле второй дифференциал инвариантным не является.

Но в К-Ф он тоже не инвариантен. Инвариантый смысл имеет, а не инвариантен. Игра слов. Я просто хочу сказать, что старшие производные являеются тензорами при линейных заменах. Вот в этом их инвариантность и состоит. Что в коордринатном виде, что в бескоординатном. Бескооординатное определение ("инвариантное") именно поэтому и возможно.

Ладно, всем всё понятно )

Pphantom · 09/05/12 25179

lena7 в сообщении #875413 писал(а):

Я не знаю, что там у Фихтенгольца, но дифференциал и производная это одно и то же. И не надо мозги засорять лишними сущностями.

Такое мнение встречается, но для приложений это крайне неудобно.

Munin · 30/01/06 72407

lena7 в сообщении #875413 писал(а):

А Фихтенгольца уже не исправлять надо, а выкидывать. Устарёл он. Особенно учитывая, что значительная часть его посвящена тому, как жить в мире, где нет компьютеров.

Да, в мире, где есть компьютеры, жить гораздо сложнее: приходится бороться ещё и со всеобщим повальным увлечением всё свалить на компьютеры.

-- 14.06.2014 21:00:24 --

Oleg Zubelevich, g______d, Padawan
Я правильно понимаю, что единственный инвариантный объект, который можно составить из вторых производных скалярной функции, - это 2-форма? (Не привлекая первых производных и связности.)

Jukier · 28/10/13 36