И в чём же отличие этих конструкций?
Отличие заключается в том, что если отвес служит указателем соответствию «вертикали», то уровень – соответствию «горизонтали» различных поверхностей конструкции при ускорении.
Итак, создаем конструкцию в виде квадрата с таким расчетом, чтобы используемые ускорения не создавали сколь-нибудь значимых ее деформаций. Вписанная в квадрат единичная окружность проградуированна с шагом 10º (см. рис. 1.1):
Представим, что такая связанная с ИСО' конструкция движется по оси

со скоростью

относительно АСО. Оси

и

совпадают. С точки зрения наблюдателей АСО – конструкция сокращена в направлении движения с коэффициентом

(на рисунках

), т.е. представляет из себя прямоугольник, с вписанным в него эллипсом (см. рис. 2.1).
Очевидно, что если теперь придать конструкции ускорение по оси

, то положение отвеса будет совпадать с осью

, как и траектория падения пробного тела (см. рис. 3.1). А поскольку углы между элементами конструкции в данном случае остались прямыми, то, если представить эллипс в виде уровня, указатель в виде пузырька в жидкости (синяя окружность) не отклонится от нулевой отметки (на оси

).
Теперь представим несколько иную ситуацию – покоящуюся относительно АСО конструкцию поворачиваем на угол
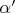
против часовой стрелки:

т.е. поворачиваем конструкцию вместе с «прилепленной» к ней системой координат на некоторый угол, скажем, на угол

(см. рис. 1.2):
Снова представим, что такая связанная с ИСО' конструкция движется по оси

с той же скоростью

относительно АСО. С точки зрения наблюдателей АСО – конструкция сжата в направлении движения, но теперь координатные оси не совпадают, а конструкция представляет из себя параллелограмм с вписанным в него эллипсом (см. рис. 2.2). Из-за особенностей распространения света в движущейся ИСО' и релятивистских эффектов, с точки зрения сопутствующих наблюдателей ИСО' конструкция остается квадратной формы, а координатные оси

и

ортогональны (см. рис. 1.1).
Поскольку ускорение будет производиться по оси

, для наглядности придаем оси

вертикальное положение (с привычными нам понятиями верх-низ при ускорении), для чего необходимо сделать еще один поворот. С помощью формул (2a, 2b) производим перерасчет значения угла
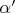
из ИСО' в АСО и, получив новое значение угла

, используем формулы:

повернув тем самым конструкцию по часовой стрелке на угол

(см.рис. 3.2).
После этого поворота получаем три системы координат:
1. Изначальная отрогональная

АСО, где ось

остается осью движения и сокращения конструкции, и именно от этой оси продолжают производиться все расчеты углов.
2. Неортогональная с сокращенными значениями

ИСО', степень сокращения вычисляется по формуле (3).
3. Отрогональная

в которой оси

и

совпадают, а оси

повернуты относительно осей

на угол

по часовой стрелке.
Очевидно, что если теперь придать конструкции ускорение по оси

, то положение отвеса будет совпадать с осью

, как и траектория падения пробного тела (см. рис. 3.2). А если представить повернутый эллипс в виде уровня, то указатель в виде пузырька в жидкости (синяя окружность) отклонится от нулевой отметки (нулевая отметка находится на оси

) на угол

(с точки зрения наблюдателей НСО'), вычисляемый по формулам (8a, 8b), т.е. угол между прямой, соединяющей начало координат с «верхней» точкой эллипса (точкой касания эллипса прямой, параллельной оси

) и осью

.
Таким образом, указатель в виде пузырька в жидкости покажет, что в действительности расположенные параллельно оси

элементы конструкции не перпендикулярны элементам, расположенным параллельно оси

. Из чего можно сделать вывод о том, что конструкция находится в движении относительно АСО, и именно абсолютным движением обусловлено сокращение конструкции и изменение углов.
Что пузырёк, что отвес - разницы нет никакой, равновесное положение указателя и там и там определяется только направлением силы тяжести и ничем другим.
Не совсем так. положение указателя уровня определяется не только направлением силы тяжести, но и сфероидальной формой сосуда с заключенной в нем жидкостью. Из представленного рисунка (см. рис. 3.2) со всей очевидностью следует, что свободно всплывающий пузырек воздуха должен двигаться по оси

, а когда достигнет стенки сосуда, должен отклониться на угол

, что и позволяет обнаружить отклонение от горизонтали соответствующих элементов конструкции.