Если

больше 2, то

.
(В самом деле, рассмотрим

и

,

.

. Найдем точку, где
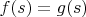
, это, очевидно,

. Очевидно так же, что

хотя бы для

. Но по известным теоремам, в таком случае, $f(s) < g(s), s > 2).
Таким образом,

.
Нууу, это уже несколько перебор, тем более, что на самом деле

. То, что неравенство

выполняется только при

, --- довольно очевидный мелкий факт (для формального доказательства производные применять, конечно, можно, но здесь это явное излишество; индукция по

была бы более адекватным средством).
Ответ

правильный, и мы действительно имеем финиш.