Помогите пожалуйста разобраться!
Условие: пусть
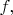

- отображения множества рациональных чисел в себя.

Найти подмножество множества рациональных чисел, содержащее ноль и все числа, являющиеся образами нуля при всевозможных отображениях, равных композиции любого конечного числа отображений

Предполагаю, что нужно рассмотреть:
1.

2.

3.

4.

Рассмотрим







Очевидно, что при всевозможных отображениях, равных композиции любого конечного числа отображений
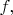
получаем множество натуральных чисел и ноль, причем, при нечетном

получаем нечетные числа, при четном - четные.
Рассмотрим




При всевозможных отображениях, равных композиции любого конечного числа отображений

получается только нуль.
Рассмотрим








Здесь наблюдение может показаться странным, но ничего другого я пока не придумала. Числитель отображения следующей степени равен сумме числителя и знаменателя предыдущей

Не знаю пока, как иначе это обозначить.
Рассмотрим

здесь получается что мы делим на ноль...но ведь нельзя?
Подскажите пожалуйста, правильным путем ли я иду, как описать

P.S. Перечитала еще раз условие задачи, подумала, что может быть не надо рассматривать

но вспомнила, что преподаватель про это упомянула.
Большое спасибо.