Очевидно

нечетно.
Проверив остатки по модулю 8, получим, что

разной четности, поэтому
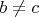
.
Пусть

. Тогда

. Следовательно,

Отсюда:

.

делится на

. Так как НОД

, то

, где число

не делится на 7. Подставляя это выражение для

в исходное равенство, получим после сокращения на

. Т.к.

, то

делится на

. Сократим обе части последнего равенства на

. В правой части равенства получим 1, а в левой - число большее 1. То есть, решений нет.