При решении задач к главе 1 т.2 Шрива у меня возник такой вопрос по стр. 4,6:
Example 1.1.4 (Infinite, independent coin-toss space).
We toss a coin infinitely many times and let
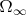
of set of possible outcomes (the set of infinite sequences of Hs and Ts). We assume the probability of head on each toss is
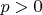
, the probability of tail is
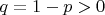
, and the different tosses are independent, a concept we define precisely in the next chapter. We want to construct a probability measure corresponding to this random experiment.
...
We create a

-algebra, called
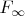
, by putting in every set that can be described in terms of finitely many coin tosses and then adding all other sets required in order to have a

-algebra. It turns out that once we specify the probability of every set that can ba described in terms of finitely many coin tosses, the probability of every set in
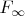
is determined. There are sets in
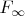
whose probability, although determined, is not easily computed. For example, consider the set

of sequences
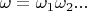
for which
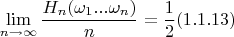
where
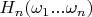
denotes the number of
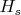
in the first

tosses. In other words,

is the set oа sequences of heads and tails for which the long-run average number of heads is

. Because its description involves all the coin tosses, it was not defined directly at any stage of the process outlined above. On the other hand, it is in
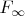
, and that means its probability is somehow determined by this process and the properties of probability measures. To see that

is in
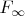
, we fix positive integers

and

define the set
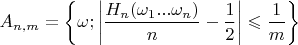
This set is in

, and once

and

are known, its probability is defined by the process outlined above. By the definition of limit, a coin-toss sequence
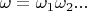
satisfies (1.1.13) if and only if for every positive integer

there exists a positive integer

such that for all

we have
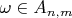
. In order words, the set of

for which (1.1.13) holds is
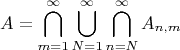
Последний вывод я не понял. Вроде бы по логике должно