Численное решение двумерного уравнения переноса

[Dhara]

Доброго времени суток, уважаемые знатоки.
Так получилось, что еще не проходя теорию дифф. уравнений (их попросту нет в программе 11 класса), пришлось столкнуться с ними. Поискав в интернете уравнение переноса для двумерного случая, я его таки нашел

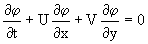
Где $U(x,y,t)$ и $V(x,y,t)$ - компоненты вектора скорости.

Перейду к задаче. У меня есть сетка N x M, для которой я задаю начальное положение вещества в клетках. С шагом времени t мне нужно численно определять содержание вещества во всей сетке (простите, если я не корректно выразился).
Я пишу программу для расчета распространения загрязнений, с уравнением диффузии я разобрался, и она работает как надо. Но вот с переносом - проблемы.

Путем проб и ошибок, я дошел до следующего решения (методом конечных разностей)
C^{k+1}_{i,j} = C^k_{i,j} + Tau ( -U \frac{C^k_{i+1,j}-C^k_{i-1,j}} {2h} -V \frac{C^k_{i,j+1}-C^k_{i,j-1}} {2h})


Где $C^{k+1}$ - значение узла на следующем шаге на следующем шаге, $Tau$ - шаг по времени, $C^k$ - начальное состояние сетки, $h$ - шаг по сетке.

Помогите, точнее направьте в какую сторону копать (лучше, конечно же, с ссылкой на конкретную литературу). Премного признателен!

[Deggial]

Тема перемещена из форума «Помогите решить / разобраться (М)» в форум «Карантин»
Причина переноса: формулы не оформлены $\TeX$ом

Dhara, наберите все формулы и термы $\TeX$ом. Инструкции по оформлению формул здесь или здесь (или в этом видеоролике).
После исправлений сообщите в теме Сообщение в карантине исправлено, и тогда тема будет возвращена.